Franck-Condon-Prinzip

Das Franck-Condon-Prinzip ist eine Regel in der Spektroskopie und Quantenchemie, die die Intensität von vibronischen Übergängen erklärt. Vibronische Übergänge sind die gleichzeitigen Änderungen der elektronischen und schwingenden Energieniveaus eines Moleküls aufgrund der Absorption oder Emission eines Photons der entsprechenden Energie. Das Prinzip besagt, dass während eines elektronischen Übergangs ein Wechsel von einem Schwingungsenergieniveau zu einem anderen wahrscheinlicher ist, wenn sich die beiden Schwingungswellenfunktionen stärker überlappen.

Zusätzliches empfohlenes Wissen

Inhalt

1 Überblick
2 Entwicklung des Prinzips
3 Quantenmechanische Formulierung
4 Franck-Condon-Metaphern in der Spektroskopie
- 4.1 Franck-Condon-Prinzip für Phononen
- 4.2 Franck-Condon-Prinzip in der Solvatation
5 Referenzen
6 Siehe auch

Übersicht

Das Franck-Condon-Prinzip hat eine gut etablierte semiklassische Interpretation, die auf den ursprünglichen Beiträgen von James Franck beruht. Elektronische Übergänge sind im Wesentlichen augenblicklich, verglichen mit der Zeitskala der Kernbewegungen. Wenn das Molekül also während des elektronischen Übergangs in ein neues Schwingungsniveau übergeht, muss dieses neue Schwingungsniveau augenblicklich mit den Kernpositionen und -impulsen des Schwingungsniveaus des Moleküls im ursprünglichen elektronischen Zustand kompatibel sein. Im semiklassischen Bild der Schwingungen (Oszillationen) eines einfachen harmonischen Oszillators können die notwendigen Bedingungen an den Wendepunkten auftreten, wo der Impuls Null ist.

Klassischerweise ist das Franck-Condon-Prinzip die Annäherung, dass ein elektronischer Übergang am wahrscheinlichsten ist, ohne dass sich die Positionen der Kerne in der molekularen Einheit und ihrer Umgebung ändern. Der sich daraus ergebende Zustand wird als Franck-Condon-Zustand bezeichnet, und der betreffende Übergang als vertikaler Übergang. Die quantenmechanische Formulierung dieses Prinzips lautet, dass die Intensität eines vibronischen Übergangs proportional zum Quadrat des Überlappungsintegrals zwischen den Schwingungswellenfunktionen der beiden an dem Übergang beteiligten Zustände ist. – IUPAC Compendium of Chemical Terminology, 2nd Edition (1997)

In der quantenmechanischen Darstellung sind die Schwingungsniveaus und die Schwingungswellenfunktionen die von harmonischen Quantenoszillatoren oder von komplexeren Annäherungen an die potentielle Energie von Molekülen, wie z. B. das Morse-Potential. Abbildung 1 veranschaulicht das Franck-Condon-Prinzip für vibronische Übergänge in einem Molekül mit Morse-ähnlichen potenziellen Energiefunktionen sowohl im Grundzustand als auch in angeregten elektronischen Zuständen. In der Tieftemperaturnäherung beginnt das Molekül im Schwingungsniveau v = 0 des elektronischen Grundzustands und geht nach Absorption eines Photons mit der erforderlichen Energie in den angeregten elektronischen Zustand über. Die Elektronenkonfiguration des neuen Zustands kann zu einer Verschiebung der Gleichgewichtslage der Kerne führen, aus denen das Molekül besteht. In der Abbildung ist diese Verschiebung der Kernkoordinaten zwischen dem Grundzustand und dem ersten angeregten Zustand mit q 10 gekennzeichnet. Im einfachsten Fall eines zweiatomigen Moleküls bezieht sich die Kernkoordinatenachse auf den Abstand zwischen den Kernen. Der vibronische Übergang ist durch einen vertikalen Pfeil gekennzeichnet, da während des Übergangs konstante Kernkoordinaten angenommen werden. Die Wahrscheinlichkeit, dass sich das Molekül in einem bestimmten Schwingungsniveau befindet, ist proportional zum Quadrat der (vertikalen) Überlappung der Schwingungswellenfunktionen des Ausgangs- und des Endzustands (siehe Abschnitt Quantenmechanische Formulierung unten). Im elektronisch angeregten Zustand entspannen sich die Moleküle schnell auf das niedrigste Schwingungsniveau (Kascha-Regel) und können von dort durch Photonenemission in den niedrigsten elektronischen Zustand zerfallen. Das Franck-Condon-Prinzip gilt sowohl für die Absorption als auch für die Fluoreszenz.

Die Anwendbarkeit des Franck-Condon-Prinzips sowohl bei der Absorption als auch bei der Fluoreszenz führt zusammen mit der Kasha-Regel zu einer ungefähren Spiegelsymmetrie, die in Abbildung 2 dargestellt ist. Die Schwingungsstruktur von Molekülen in einem kalten, dünn besiedelten Gas ist am deutlichsten zu erkennen, da die einzelnen Übergänge nicht inhomogen verbreitert sind. Die vibronischen Übergänge sind in Abbildung 2 als schmale, gleichmäßig beabstandete Lorentzsche Linien gezeichnet. Gleiche Abstände zwischen den Schwingungsniveaus gelten nur für das parabolische Potenzial einfacher harmonischer Oszillatoren; bei realistischeren Potenzialen, wie den in Abbildung 1 dargestellten, nimmt der Energieabstand mit zunehmender Schwingungsenergie ab. Elektronische Übergänge zu und von den niedrigsten Schwingungszuständen werden oft als 0-0-Übergänge (Null-Null-Übergänge) bezeichnet und haben sowohl bei der Absorption als auch bei der Fluoreszenz die gleiche Energie.

Entwicklung des Prinzips

In einem 1926 in den Transactions of the Faraday Society veröffentlichten Bericht befasste sich James Franck mit den Mechanismen von photoneninduzierten chemischen Reaktionen. Der vermutete Mechanismus war die Anregung eines Moleküls durch ein Photon, gefolgt von einer Kollision mit einem anderen Molekül während der kurzen Zeit der Anregung. Die Frage war, ob ein Molekül in einem einzigen Schritt, der Absorption eines Photons, und ohne Zusammenstoß in Photoprodukte zerfallen kann. Damit ein Molekül auseinanderbrechen kann, muss es von dem Photon eine Schwingungsenergie erhalten, die die Dissoziationsenergie übersteigt, d. h. die Energie zum Aufbrechen einer chemischen Bindung. Damals war jedoch bekannt, dass Moleküle nur Energie absorbieren, die zulässigen Quantenübergängen entspricht, und dass es keine Schwingungsniveaus oberhalb des Dissoziationsenergieniveaus des Potenzialtopfs gibt. Die Absorption von Photonen mit hoher Energie führt zu einem Übergang in einen höheren elektronischen Zustand anstelle einer Dissoziation. Als er untersuchte, wie viel Schwingungsenergie ein Molekül erhalten könnte, wenn es zu einem höheren elektronischen Niveau angeregt wird, und ob diese Schwingungsenergie ausreichen könnte, um das Molekül sofort aufzubrechen, zeichnete er drei Diagramme, die die möglichen Änderungen der Bindungsenergie zwischen dem niedrigsten elektronischen Zustand und höheren elektronischen Zuständen darstellen.

Diagramm I. zeigt eine starke Abschwächung der Bindung bei einem Übergang vom Normalzustand n zu den angeregten Zuständen a und a‘. Hier haben wir D > D‘ und D‘ > D“. Gleichzeitig verschiebt sich die Gleichgewichtslage der Kerne mit der Anregung zu größeren Werten von r. Wenn wir von der Gleichgewichtslage (dem Minimum der potentiellen Energie) der n-Kurve senkrecht nach oben zu den a-Kurven in Diagramm I. gehen, haben die Teilchen eine potentielle Energie größer als D‘ und fliegen auseinander. In diesem Fall haben wir eine sehr große Änderung der Schwingungsenergie bei der Anregung durch Licht… – James Franck 1926

James Franck erkannte, dass Änderungen in den Schwingungsniveaus eine Folge der augenblicklichen Natur der Anregung zu höheren elektronischen Energieniveaus und einer neuen Gleichgewichtsposition für das nukleare Wechselwirkungspotential sein könnten. Edward Condon erweiterte diese Erkenntnis in einem Artikel in der Physical Review aus dem Jahr 1926 mit dem Titel „A Theory of Intensity Distribution in Band Systems“ (Eine Theorie der Intensitätsverteilung in Bandsystemen) über Fotoreaktionen hinaus. Hier formuliert er die semiklassische Formulierung in einer Art und Weise, die ihrer modernen Form recht ähnlich ist. Der erste gemeinsame Verweis auf Franck und Condon in Bezug auf das neue Prinzip erscheint in derselben Ausgabe der Physical Review von 1926 in einem Artikel über die Bandstruktur von Kohlenmonoxid von Raymond Birge.

Quantenmechanische Formulierung

Betrachten wir einen elektrischen Dipolübergang vom anfänglichen Schwingungszustand (ʋ) des elektronischen Grundniveaus (ε), 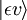$|\epsilon v\rangle$ , zu einem Schwingungszustand (ʋ‘ ) eines angeregten elektronischen Niveaus (ε‘), 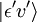$|\epsilon' v'\rangle$ (siehe Bra-ket-Notation). Der molekulare Dipoloperator μ wird durch die Ladungen (-e) und Orte (ri) der Elektronen sowie die Ladungen (+eZj) und Orte (Rj) der Kerne bestimmt:

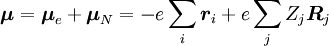
$\boldsymbol{\mu} = \boldsymbol{\mu} _e + \boldsymbol{\mu} _N = - e\sum\limits_i {\boldsymbol{r}_i } + e\sum\limits_j {Z_j \boldsymbol{R}_j }$

Die Wahrscheinlichkeitsamplitude P für den Übergang zwischen diesen beiden Zuständen ist gegeben durch

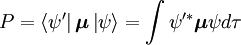
$P = \left\langle \psi'\right|\boldsymbol{\mu} \left| \psi \right\rangle =\int {\psi'^ *} \boldsymbol{\mu} \psi d\tau$

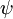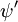Wobei $\psi\$ und $\psi'\$ die Gesamtwellenfunktionen des Anfangs- bzw. Endzustandes sind. Die Gesamtwellenfunktionen sind das Produkt der einzelnen Schwingungs- (abhängig von den Raumkoordinaten der Kerne) und elektronischen Raum- und Spin-Wellenfunktionen:

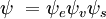
$\psi\ = \psi _e \psi _v \psi _s$

Diese Trennung der elektronischen und der Schwingungswellenfunktionen ist ein Ausdruck der Born-Oppenheimer-Näherung und ist die Grundannahme des Franck-Condon-Prinzips. Die Kombination dieser Gleichungen führt zu einem Ausdruck für die Wahrscheinlichkeitsamplitude in Form von getrennten elektronischen Raum-, Spin- und Schwingungsbeiträgen:

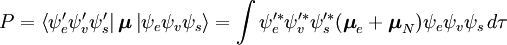
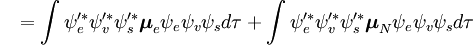
$P=\left\langle \psi _e' \psi _v' \psi _s' \right|\boldsymbol{\mu} \left| \psi _e \psi _v \psi _s \right\rangle =\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} (\boldsymbol{\mu} _e + \boldsymbol{\mu} _N) \psi _e \psi _v \psi _s \, d\tau$ ${\color{White}P}=\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} \boldsymbol{\mu} _e \psi _e \psi _v \psi _s d\tau +\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} \boldsymbol{\mu} _N \psi _e \psi _v \psi _s d\tau$ ${\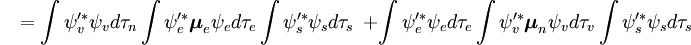color{White}P}=\int { \psi _v'^ * } \psi _v d\tau_n \int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e \int { \psi _s'^ * } \psi _s d\tau_s \ \ + \int { \psi _e'^ * } \psi _e d\tau_e \int { \psi _v'^ * } \boldsymbol{\mu} _n \psi _v d\tau_v \int { \psi _s'^ * } \psi _s d\tau_s$ ${\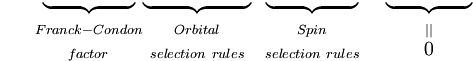color{White}P=} \begin{matrix} \underbrace{ {\color{White}.................} } \\ {}_{Franck-Condon} \\ {}_{Faktor} \end{matrix} \begin{matrix} \underbrace{{color{White}....................} } \\ {}_{Orbital} \\ {}_{Auswahl}regeln} \end{matrix} \ \ \begin{matrix} \underbrace{ {\color{White}.................} } \\ {}_{Spin} \\ {}_{Auswahl}regeln} \end{matrix} \ \ \ \ \begin{matrix} \underbrace{ {\color{White}................} } \\ {}_{||} \\ 0 \end{matrix}$

Der spin-unabhängige Teil des Anfangsintegrals wird hier als Produkt zweier Integrale angenähert

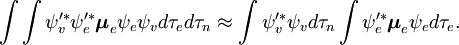
$\int\int { \psi _v'^ * } { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e \psi _v d\tau_e d\tau_n \approx \int{ \psi _v'^ * } \psi _vd\tau_n \int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e .$

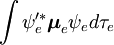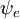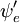Diese Faktorisierung wäre exakt, wenn das Integral $\int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e$ über die Raumkoordinaten der Elektronen nicht von den Kernkoordinaten abhängen würde. In der Born-Oppenheimer-Approximation hängen $\psi_e\,$ und $\psi'_e\,$ jedoch (parametrisch) von den Kernkoordinaten ab, so dass das Integral (eine sogenannte Übergangsdipolfläche) eine Funktion der Kernkoordinaten ist. Da die Abhängigkeit in der Regel recht glatt ist, wird ihre Vernachlässigung (d.h. die Annahme, dass die Übergangsdipolfläche unabhängig von den Kernkoordinaten ist) oft zugelassen.

Das erste Integral nach dem Pluszeichen ist gleich Null, da die elektronischen Wellenfunktionen verschiedener Zustände orthogonal sind. Der Rest ist das Produkt aus drei Integralen. Das erste Integral ist das Schwingungsüberlappungsintegral, auch Franck-Condon-Faktor genannt. Die beiden verbleibenden Integrale, die zur Wahrscheinlichkeitsamplitude beitragen, bestimmen die elektronischen Raum- und Spin-Selektionsregeln.

Das Franck-Condon-Prinzip ist eine Aussage über erlaubte Schwingungsübergänge zwischen zwei verschiedenen elektronischen Zuständen, andere quantenmechanische Selektionsregeln können die Wahrscheinlichkeit eines Übergangs verringern oder ihn ganz verbieten. Rotationsselektionsregeln wurden in der obigen Herleitung vernachlässigt. Rotationsbeiträge können in den Spektren von Gasen beobachtet werden, sind aber in Flüssigkeiten und Festkörpern stark unterdrückt.

Es sollte klar sein, dass die quantenmechanische Formulierung des Franck-Condon-Prinzips das Ergebnis einer Reihe von Näherungen ist, vor allem der Annahme des elektrischen Dipolübergangs und der Born-Oppenheimer-Näherung. Schwächere magnetische Dipol- und elektrische Quadrupol-Elektronenübergänge sowie die unvollständige Gültigkeit der Faktorisierung der Gesamtwellenfunktion in Kern-, elektronische Raum- und Spin-Wellenfunktionen bedeuten, dass die Auswahlregeln, einschließlich des Franck-Condon-Faktors, nicht streng eingehalten werden. Für jeden gegebenen Übergang wird der Wert von P durch alle Selektionsregeln bestimmt, wobei die Spinselektion den größten Beitrag leistet, gefolgt von den elektronischen Selektionsregeln. Der Franck-Condon-Faktor moduliert die Intensität von Übergängen nur schwach, d. h. er trägt mit einem Faktor in der Größenordnung von 1 zur Intensität von Banden bei, deren Größenordnung durch die anderen Auswahlregeln bestimmt wird. In der nachstehenden Tabelle ist der Bereich der Extinktionskoeffizienten für die möglichen Kombinationen von erlaubten und verbotenen Spin- und Orbitalauswahlregeln angegeben.

Intensitäten elektronischer Übergänge

Wertebereich des Extinktionskoeffizienten (ε) (moles-1 cm-1)

Spin und Orbital erlaubt

103 bis 105

Spin erlaubt aber Orbital verboten

100 bis 103

Spin verboten aber Orbital erlaubt

10-5 bis 100

Franck-Condon Metaphern in der Spektroskopie

Das Franck-Condon Prinzip, gilt in seiner kanonischen Form nur für Änderungen der Schwingungsniveaus eines Moleküls im Zuge einer Änderung der elektronischen Niveaus durch Absorption oder Emission eines Photons. Die physikalische Intuition dieses Prinzips beruht auf der Vorstellung, dass die Kernkoordinaten der Atome, aus denen das Molekül besteht, keine Zeit haben, sich während der sehr kurzen Zeitspanne eines elektronischen Übergangs zu ändern. Diese physikalische Intuition kann jedoch auf die Wechselwirkungen zwischen lichtabsorbierenden oder -emittierenden Molekülen (Chromophoren) und ihrer Umgebung ausgedehnt werden, und dies geschieht auch routinemäßig. Franck-Condon-Metaphern sind angemessen, weil Moleküle oft stark mit den sie umgebenden Molekülen wechselwirken, insbesondere in Flüssigkeiten und Festkörpern, und diese Wechselwirkungen die Kernkoordinaten des Chromophors in einer Weise verändern, die den vom Franck-Condon-Prinzip berücksichtigten Molekülschwingungen sehr ähnlich ist.

Franck-Condon-Prinzip für Phononen

Die engste Franck-Condon-Analogie ergibt sich aus der Wechselwirkung von Phononen – Quanten von Gitterschwingungen – mit den elektronischen Übergängen von Chromophoren, die als Verunreinigungen in das Gitter eingebettet sind. In dieser Situation können Übergänge zu höheren elektronischen Niveaus stattfinden, wenn die Energie des Photons der rein elektronischen Übergangsenergie oder der rein elektronischen Übergangsenergie plus der Energie eines oder mehrerer Gitterphononen entspricht. In der Tieftemperaturnäherung erfolgt die Emission vom Null-Phonon-Niveau des angeregten Zustands zum Null-Phonon-Niveau des Grundzustands oder zu höheren Phononenniveaus des Grundzustands. Wie beim Franck-Condon-Prinzip wird die Wahrscheinlichkeit von Übergängen, an denen Phononen beteiligt sind, durch die Überlappung der Phononenwellenfunktionen auf dem Anfangs- und dem Endenergieniveau bestimmt. Bei der Anwendung des Franck-Condon-Prinzips auf Phononenübergänge wird die Beschriftung der horizontalen Achse von Abbildung 1 in Abbildung 6 durch die Konfigurationskoordinate für eine normale Mode ersetzt. Die potentielle Energie der Gittermode qi in Abbildung 6 wird als die eines harmonischen Oszillators dargestellt, und der Abstand zwischen den Phononenniveaus (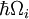 $\hbar \Omega _i$ ) wird durch Gitterparameter bestimmt. Da die Energie einzelner Phononen im Allgemeinen recht klein ist, können Null- oder Wenig-Phononen-Übergänge nur bei Temperaturen unter etwa 40 Kelvin beobachtet werden.

Weitere Einzelheiten und Referenzen siehe Null-Phononen-Linie und Phononenseitenband.

Franck-Condon-Prinzip in der Solvatation

Franck-Condon-Überlegungen können auch auf die elektronischen Übergänge von in Flüssigkeiten gelösten Chromophoren angewendet werden. Bei dieser Anwendung der Franck-Condon-Metapher tragen die Schwingungsniveaus der Chromophore sowie die Wechselwirkungen der Chromophore mit Phononen in der Flüssigkeit weiterhin zur Struktur der Absorptions- und Emissionsspektren bei, aber diese Effekte werden getrennt und unabhängig voneinander betrachtet.

Betrachten wir Chromophore, die von Lösungsmittelmolekülen umgeben sind. Diese umgebenden Moleküle können mit den Chromophoren in Wechselwirkung treten, insbesondere wenn die Lösungsmittelmoleküle polar sind. Diese Assoziation zwischen Lösungsmittel und gelöstem Stoff wird als Solvatation bezeichnet und ist eine stabilisierende Wechselwirkung, d. h. die Lösungsmittelmoleküle können sich so lange bewegen und drehen, bis die Energie der Wechselwirkung minimiert ist. Die Wechselwirkung selbst umfasst elektrostatische und van-der-Waals-Kräfte und kann auch Wasserstoffbrückenbindungen einschließen. Das Franck-Condon-Prinzip kann angewendet werden, wenn die Wechselwirkungen zwischen dem Chromophor und den umgebenden Lösungsmittelmolekülen im Grundzustand und im angeregten elektronischen Zustand unterschiedlich sind. Diese Veränderung der Wechselwirkung kann beispielsweise durch unterschiedliche Dipolmomente in diesen beiden Zuständen entstehen. Wenn das Chromophor zunächst in seinem Grundzustand nahe am Gleichgewicht mit den umgebenden Lösungsmittelmolekülen ist und dann ein Photon absorbiert, das es in den angeregten Zustand bringt, ist seine Wechselwirkung mit dem Lösungsmittel im angeregten Zustand weit vom Gleichgewicht entfernt. Dieser Effekt entspricht dem ursprünglichen Franck-Condon-Prinzip: Der elektronische Übergang ist sehr schnell im Vergleich zur Bewegung der Kerne – der Umlagerung der Lösungsmittelmoleküle im Falle der Solvatation -. Wir sprechen jetzt von einem vertikalen Übergang, aber die horizontale Koordinate ist jetzt der Lösungsmittel-Lösungsmittel-Wechselwirkungsraum. Diese Koordinatenachse wird oft als „Solvationskoordinate“ bezeichnet und stellt, etwas abstrakt, alle relevanten Bewegungsdimensionen aller wechselwirkenden Lösungsmittelmoleküle dar.

Beim ursprünglichen Franck-Condon-Prinzip beginnen die Moleküle, die sich in höheren Schwingungszuständen befinden, nach dem elektronischen Übergang sofort, in den niedrigsten Schwingungszustand zu entspannen. Im Falle der Solvatation versuchen die Lösungsmittelmoleküle sofort, sich neu anzuordnen, um die Wechselwirkungsenergie zu minimieren. Die Geschwindigkeit der Lösungsmittelrelaxation hängt von der Viskosität des Lösungsmittels ab. Unter der Annahme, dass die Relaxationszeit des Lösungsmittels im Vergleich zur Lebensdauer des elektronisch angeregten Zustands kurz ist, erfolgt die Emission aus dem Zustand mit der niedrigsten Lösungsmittelenergie des angeregten elektronischen Zustands. Bei Lösungsmitteln für kleine Moleküle wie Wasser oder Methanol bei Raumtemperatur liegt die Lösungsmittelrelaxationszeit in der Größenordnung von einigen zehn Pikosekunden, während die Lebensdauer des angeregten Zustands des Chromophors zwischen einigen Pikosekunden und einigen Nanosekunden liegt. Unmittelbar nach dem Übergang in den elektronischen Grundzustand müssen sich auch die Lösungsmittelmoleküle neu anordnen, um die neue elektronische Konfiguration des Chromophors aufzunehmen. Abbildung 7 veranschaulicht die Anwendung des Franck-Condon-Prinzips auf die Solvatation. Wenn die Lösung mit Licht beleuchtet wird, das der elektronischen Übergangsenergie entspricht, gehen einige der Chromophore in den angeregten Zustand über. Innerhalb dieser Gruppe von Chromophoren gibt es eine statistische Verteilung der Wechselwirkungsenergien zwischen Lösungsmittel und Chromophor, die in der Abbildung durch eine Gaußsche Verteilungsfunktion dargestellt ist. Die Lösungsmittel-Chromophor-Wechselwirkung ist in beiden elektronischen Zuständen als parabolisches Potenzial dargestellt. Da der elektronische Übergang auf der Zeitskala der Lösemittelbewegung (vertikaler Pfeil) im Wesentlichen augenblicklich erfolgt, ist die Ansammlung von Chromophoren im angeregten Zustand sofort weit vom Gleichgewicht entfernt. Die Neuanordnung der Lösungsmittelmoleküle entsprechend der neuen potentiellen Energiekurve wird durch die gebogenen Pfeile in Abbildung 7 dargestellt. Man beachte, dass die elektronischen Übergänge quantisiert sind, während die Wechselwirkungsenergie zwischen Chromophor und Lösungsmittel aufgrund der großen Anzahl der beteiligten Moleküle als klassisches Kontinuum behandelt wird. Obwohl die Emission ab dem Minimum des Wechselwirkungspotenzials zwischen Chromophor und Lösungsmittel im angeregten Zustand dargestellt ist, kann eine signifikante Emission stattfinden, bevor das Gleichgewicht erreicht ist, wenn die Viskosität des Lösungsmittels hoch oder die Lebensdauer des angeregten Zustands kurz ist. Die in Abbildung 7 dargestellte Energiedifferenz zwischen absorbierten und emittierten Photonen ist der Beitrag der Solvatation zur Stokes-Verschiebung.

Fachzeitschriftenlinks erfordern möglicherweise ein Abonnement.

Franck, J. (1926). „Elementare Prozesse der photochemischen Reaktionen“. Transactions of the Faraday Society 21: 536-542. Link
Condon, E. (1926). „A theory of intensity distribution in band systems (Meeting abstract)“. Physical Review 27: 640.
Condon, E. (1926). „A theory of intensity distribution in band systems“. Physical Review 28: 1182-1201. Link
Condon, E. (1928). „Nuclear motions associated with electron transitions in diatomic molecules“. Physical Review 32: 858-872. Link
Birge, R. T. (1926). „The band spectra of carbon monoxide“. Physical Review 28: 1157-1181. Link
Noyes, W. A. (1933). „Die Korrelation von Spektroskopie und Photochemie“. Reviews of Modern Physics 5: 280-287. Link
Coolidge, A. S, James, H. M. und Present, R. D. (1936). „A study of the Franck-Condon Principle“. Journal of Chemical Physics 4: 193-211. Link
Herzberg, Gerhard (1971). Die Spektren und Strukturen der einfachen freien Radikale. New York: Dover. ISBN 0-486-65821-X.
Harris, Daniel C.; Michael D. Bertolucci (1978). Symmetry and spectroscopy. New York: Dover. ISBN 0-486-66144-X.
Bernath, Peter F. (1995). Spektren von Atomen und Molekülen (Topics in Physical Chemistry). Oxford: Oxford University Press. ISBN 0-19-507598-6.
Atkins, P. W.; R. S. Frieman (1999). Molecular Quantum Mechanics. Oxford: Oxford University Press. ISBN 0-19-855947-X.

Siehe auch

Born-Oppenheimer-Approximation
Molekulare elektronische Übergänge
Ultraviolett-sichtbare Spektroskopie
Quantenharmonischer Oszillator
Morse-Potential
Vibronische Kopplung
Null-Phonon-Linie und Phonon-Seitenband
Plötzliche Approximation

Kategorien: Quantenchemie | Spektroskopie | Molekülphysik