
A transformação de dados é um dos passos fundamentais na parte do processamento de dados. Quando eu aprendi a técnica de escala de características, os termos escala, padronização e normalização estão sendo usados com frequência. No entanto, foi bastante difícil encontrar informações sobre qual deles eu deveria usar e também quando usar. Portanto, vou explicar os seguintes aspectos chave neste artigo:
- a diferença entre a normalização e a normalização
- quando usar a normalização e quando usar a normalização
- como aplicar a escala de características em Python
O que significa a escala de características?
Na prática, encontramos frequentemente diferentes tipos de variáveis no mesmo conjunto de dados. Uma questão significativa é que o intervalo das variáveis pode ser muito diferente. Usando a escala original pode colocar mais pesos nas variáveis com um grande intervalo. Para lidar com este problema, precisamos aplicar a técnica de redimensionamento de características a variáveis independentes ou características de dados na etapa de pré-processamento de dados. Os termos normalização e padronização são às vezes usados de forma intercambiável, mas geralmente referem-se a coisas diferentes.
O objetivo da aplicação da Escala de Recursos é garantir que os recursos estejam na mesma escala, de modo que cada recurso seja igualmente importante e facilite o processamento pela maioria dos algoritmos ML.
Exemplo
Este é um conjunto de dados que contém uma variável independente (Comprado) e 3 variáveis dependentes (País, Idade e Salário). Podemos facilmente notar que as variáveis não estão na mesma escala porque o intervalo de Idade é de 27 a 50, enquanto que o intervalo de Salário vai de 48 K a 83 K. O intervalo de Salário é muito mais amplo do que o intervalo de Idade. Isto causará alguns problemas nos nossos modelos, uma vez que muitos modelos de aprendizagem de máquinas, tais como o agrupamento de k significaans e a classificação do vizinho mais próximo são baseados na Distância Euclidiana.
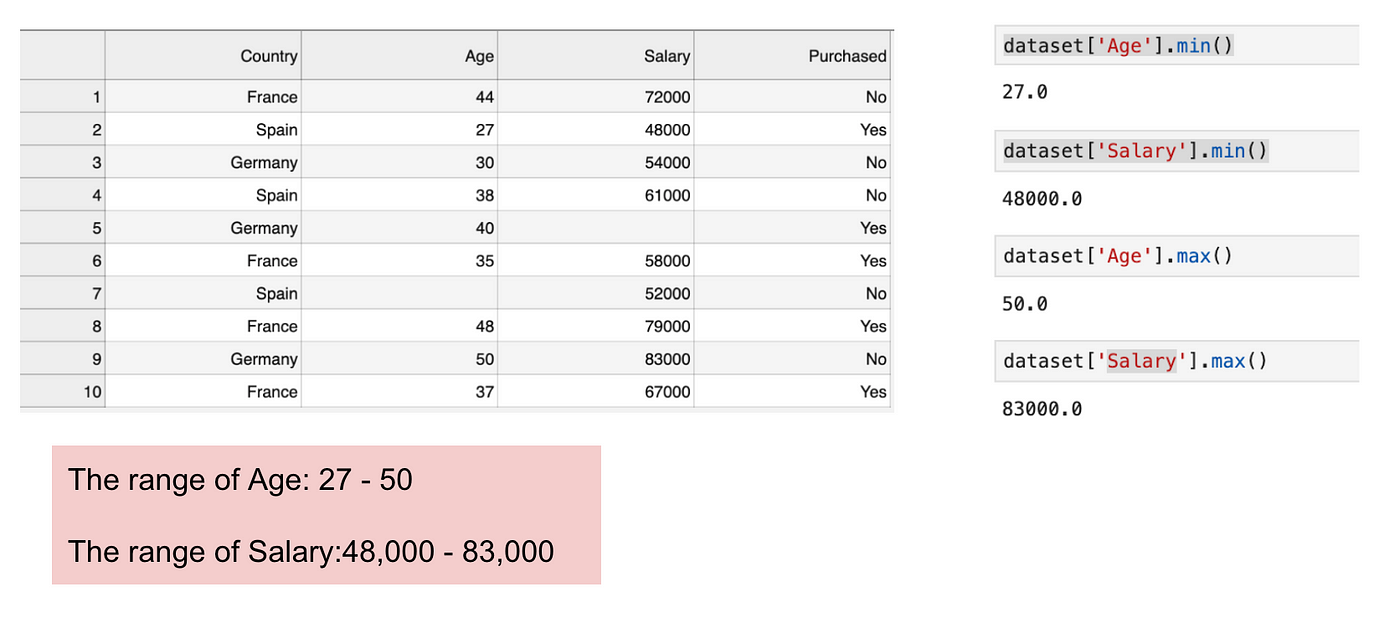
Focalização na idade e no salário.
Quando calculamos a equação da distância euclidiana, o número de (x2-x1)² é muito maior que o número de (y2-y1)² o que significa que a distância euclidiana será dominada pelo salário se não aplicarmos a escala de característica. A diferença de idade contribui menos para a diferença geral. Portanto, devemos usar a escala de característica para trazer todos os valores à mesma magnitudes e, assim, resolver esta questão. Para isso, existem principalmente dois métodos chamados Normalização e Normalização.

Euclidean aplicação de distância.
Padronização
O resultado da normalização (ou normalização Z-score) é que as características serão redimensionadas para garantir que a média e o desvio padrão sejam 0 e 1, respectivamente. A equação é mostrada abaixo:
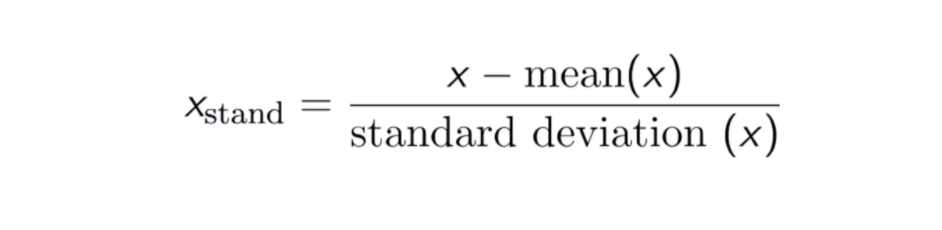
Esta técnica é para redimensionar o valor das características com o valor de distribuição entre 0 e 1 é útil para os algoritmos de otimização, tais como descida de gradiente, que são usados dentro de algoritmos de aprendizagem de máquinas que pesam entradas (por exemplo, regressão e redes neurais). O redimensionamento também é usado para algoritmos que usam medidas de distância, por exemplo, K-Nearest-Neighbours (KNN).
Código
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Normalização Máx-Min
Outra abordagem comum é a chamada Normalização Máx-Min (Escala Mín-Máx). Esta técnica consiste em redimensionar as características com um valor de distribuição entre 0 e 1. Para cada característica, o valor mínimo dessa característica é transformado em 0, e o valor máximo é transformado em 1. A equação geral é mostrada abaixo:
>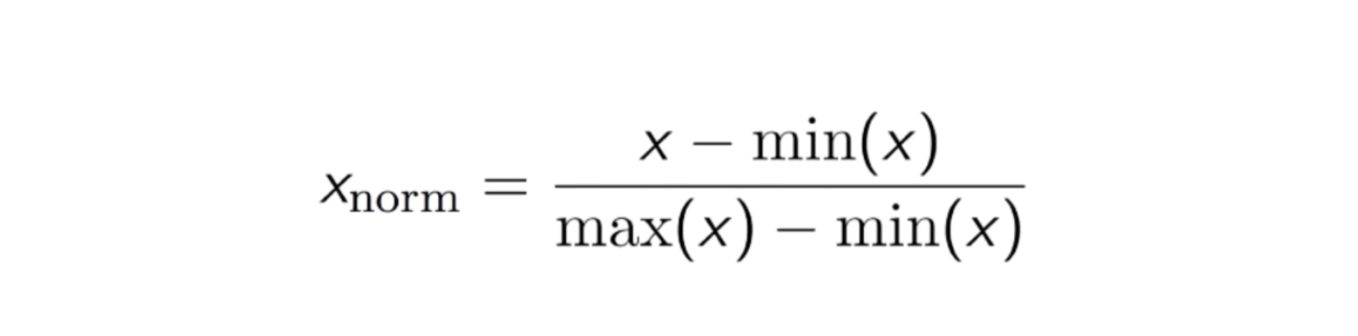
A equação de Normalização Máx-Min.
Código
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
Padrão vs Max-Min Normalização
Em contraste com a normalização, vamos obter desvios padrão menores através do processo de Max-Min Normalização. Deixe-me ilustrar mais nesta área usando o conjunto de dados acima.
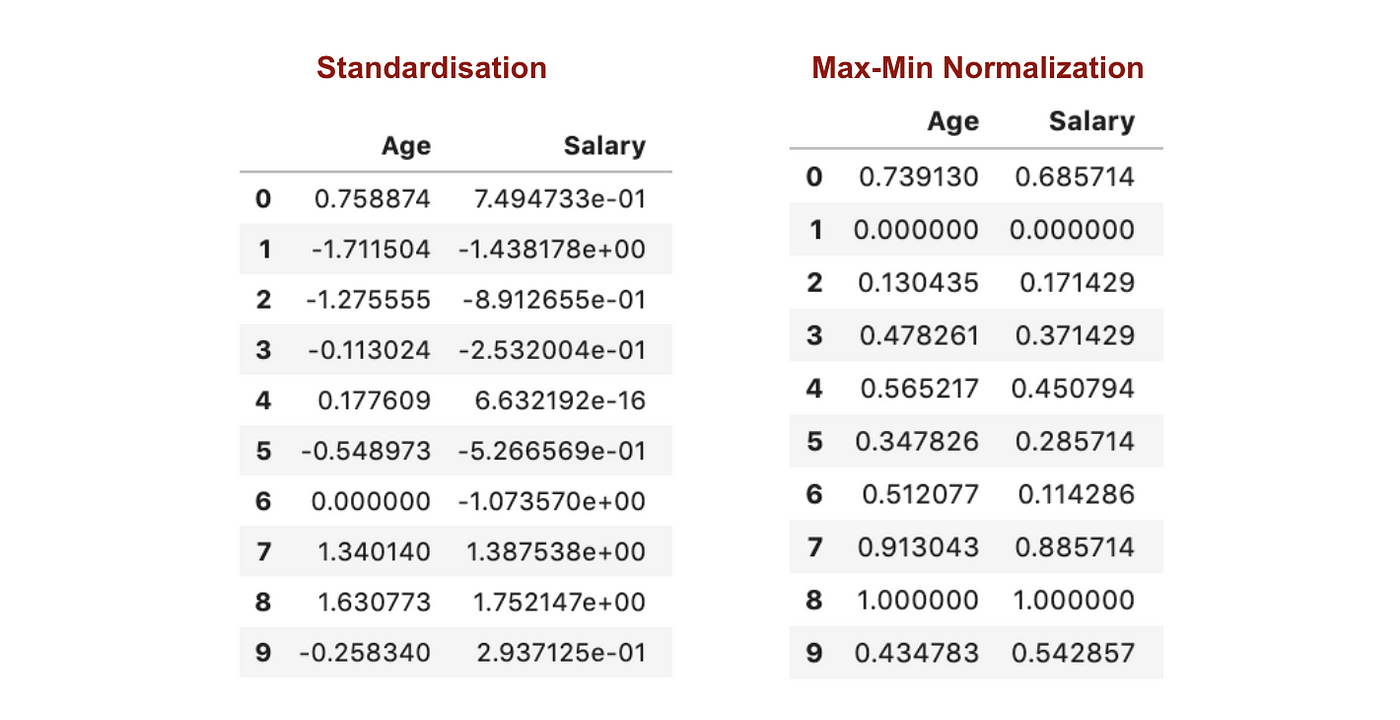
Após a escala de característica.

Distribuição Normal e Desvio Padrão de Idade.
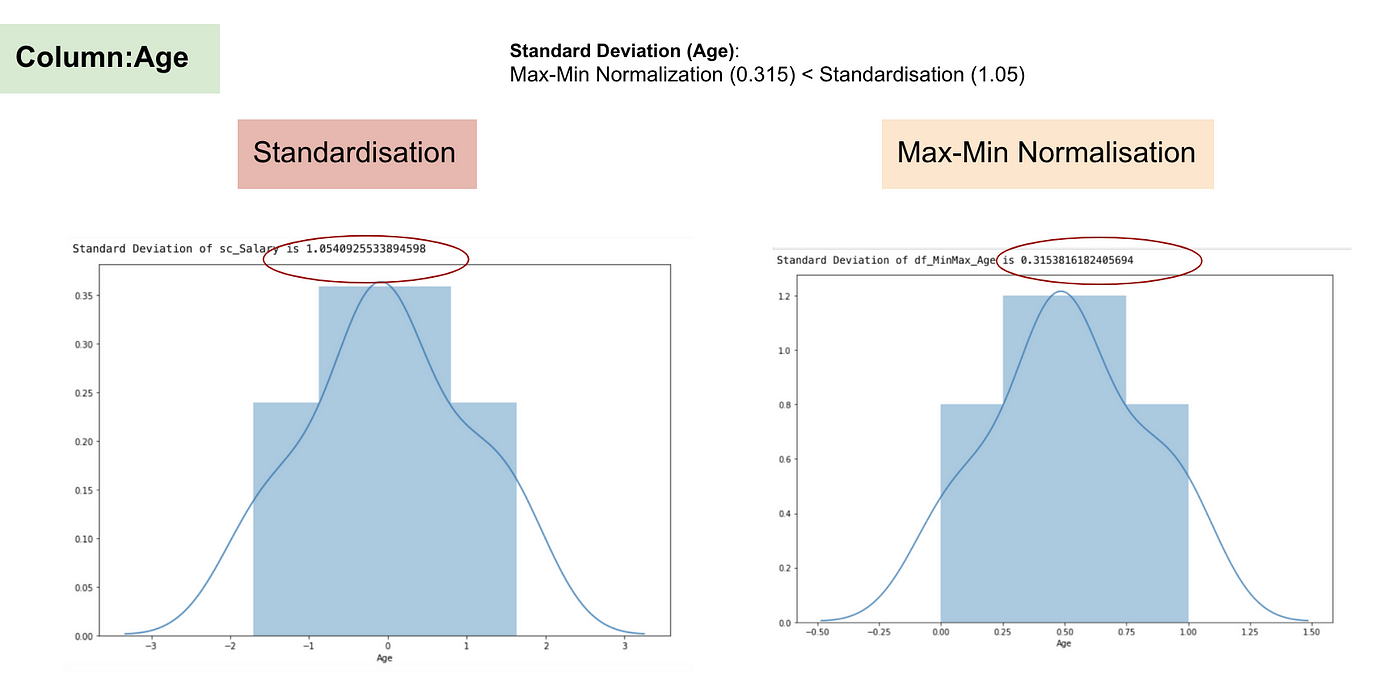
Distribuição Normal e Desvio Padrão de Idade.
Dos gráficos acima, podemos notar claramente que a aplicação da Nomaralização Max-Min no nosso conjunto de dados gerou desvios padrão menores (Salário e Idade) do que a utilização do método de Padronização. Isso implica que os dados estão mais concentrados em torno da média se escalarmos os dados usando a Nomaralização Max-Min.
Como resultado, se você tiver outliers em sua característica (coluna), normalizando seus dados irá escalar a maioria dos dados para um pequeno intervalo, o que significa que todas as características terão a mesma escala, mas não lida bem com outliers. A padronização é mais robusta para outliers, e em muitos casos, é preferível à Max-Min Normalisation.
Quando a escala de recurso importa

Alguns modelos de aprendizagem de máquina são fundamentalmente baseados em matriz de distância, também conhecida como classificador baseado em distância, por exemplo, K-Nearest-Neighbours, SVM, e Neural Network. A escala de características é extremamente essencial para esses modelos, especialmente quando o alcance das características é muito diferente. Caso contrário, características com um grande alcance terão uma grande influência no cálculo da distância.
Max-Min Normalisation tipicamente nos permite transformar os dados com escalas variáveis para que nenhuma dimensão específica domine as estatísticas, e não é necessário fazer uma suposição muito forte sobre a distribuição dos dados, tais como vizinhos k-nearest e redes neurais artificiais. No entanto, a normalização não trata muito bem os outliners. Pelo contrário, a normalização permite aos utilizadores lidar melhor com os outliers e facilitar a convergência de alguns algoritmos computacionais, como a descida de gradientes. Portanto, normalmente preferimos a padronização em vez da Normalização Min-Max.
Exemplo: Que algoritmos precisam de escala de característica
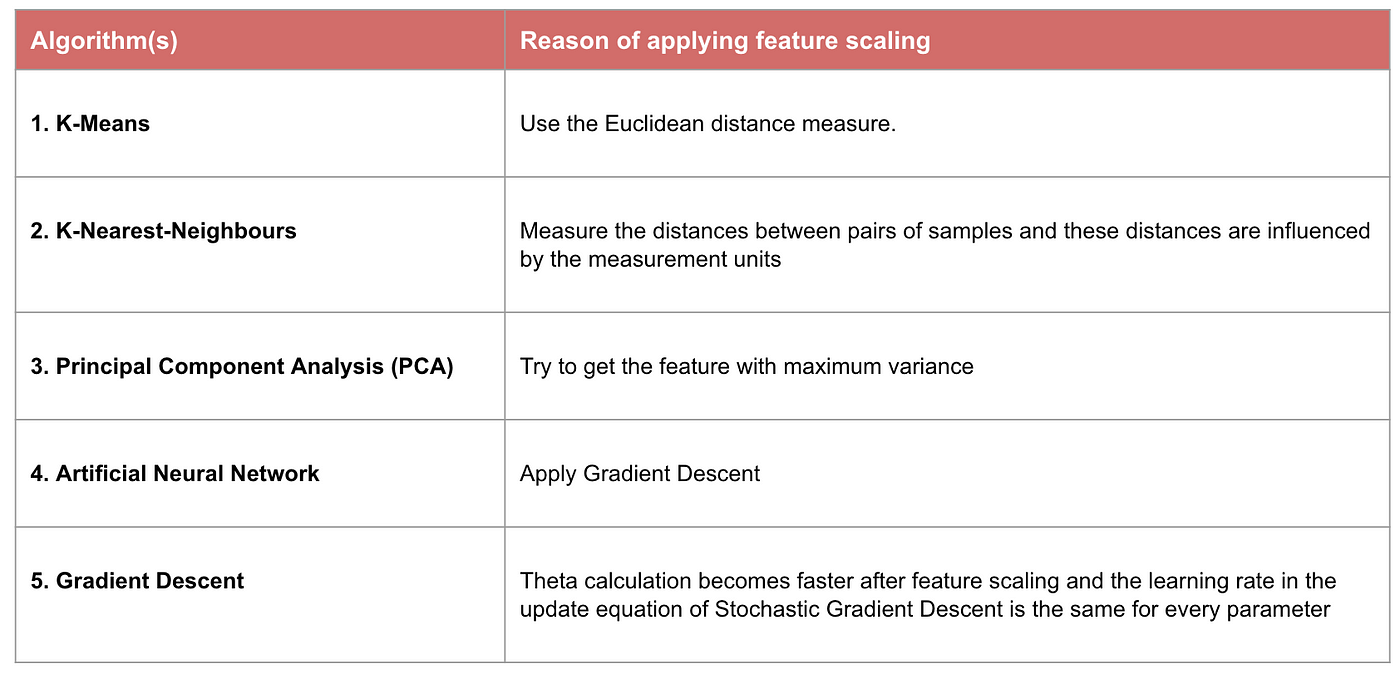
Nota: Se um algoritmo não é baseado na distância, a escala de característica não é importante, incluindo Naive Bayes, Linear Discriminant Analysis, e modelos baseados em árvores (aumento de gradiente, floresta aleatória, etc.).
Resumo: Agora você deve saber
- o objetivo de usar a escala de característica
- a diferença entre Padronização e Normalização
- os algoritmos que precisam aplicar Padronização ou Normalização
- aplicar a escala de característica em Python
Por favor encontre o código e o conjunto de dados aqui.