
Transformacja danych jest jednym z podstawowych kroków w części przetwarzania danych. Kiedy po raz pierwszy nauczyłem się techniki skalowania cech, często używane są terminy scale, standardise i normalise. Jednak dość trudno było znaleźć informacje o tym, których z nich powinienem użyć, a także kiedy ich użyć. Dlatego w tym artykule wyjaśnię następujące kluczowe aspekty:
- różnica między normalizacją a normalizacją
- kiedy używać normalizacji, a kiedy normalizacji
- jak zastosować skalowanie cech w Pythonie
Co oznacza skalowanie cech?
W praktyce często spotykamy się z różnymi typami zmiennych w tym samym zbiorze danych. Istotnym problemem jest to, że zakresy zmiennych mogą się znacznie różnić. Użycie oryginalnej skali może spowodować, że zmienne o dużym zakresie będą miały większą wagę. Aby poradzić sobie z tym problemem, musimy zastosować technikę przeskalowania cech do zmiennych niezależnych lub cech danych w kroku wstępnego przetwarzania danych. Terminy normalizacja i standaryzacja są czasami używane zamiennie, ale zazwyczaj odnoszą się do różnych rzeczy.
Celem zastosowania techniki przeskalowania cech jest upewnienie się, że cechy są na prawie tej samej skali, tak aby każda cecha była równie ważna i ułatwiała przetwarzanie przez większość algorytmów ML.
Przykład
Jest to zbiór danych, który zawiera zmienną niezależną (Zakupiony) i 3 zmienne zależne (Kraj, Wiek i Wynagrodzenie). Możemy łatwo zauważyć, że zmienne nie są na tej samej skali, ponieważ zakres wieku wynosi od 27 do 50, podczas gdy zakres wynagrodzenia wynosi od 48 K do 83 K. Zakres wynagrodzenia jest znacznie szerszy niż zakres wieku. Spowoduje to pewne problemy w naszych modelach, ponieważ wiele modeli uczenia maszynowego, takich jak klasteryzacja k-średnich i klasyfikacja najbliższych sąsiadów, opiera się na odległości euklidesowej.
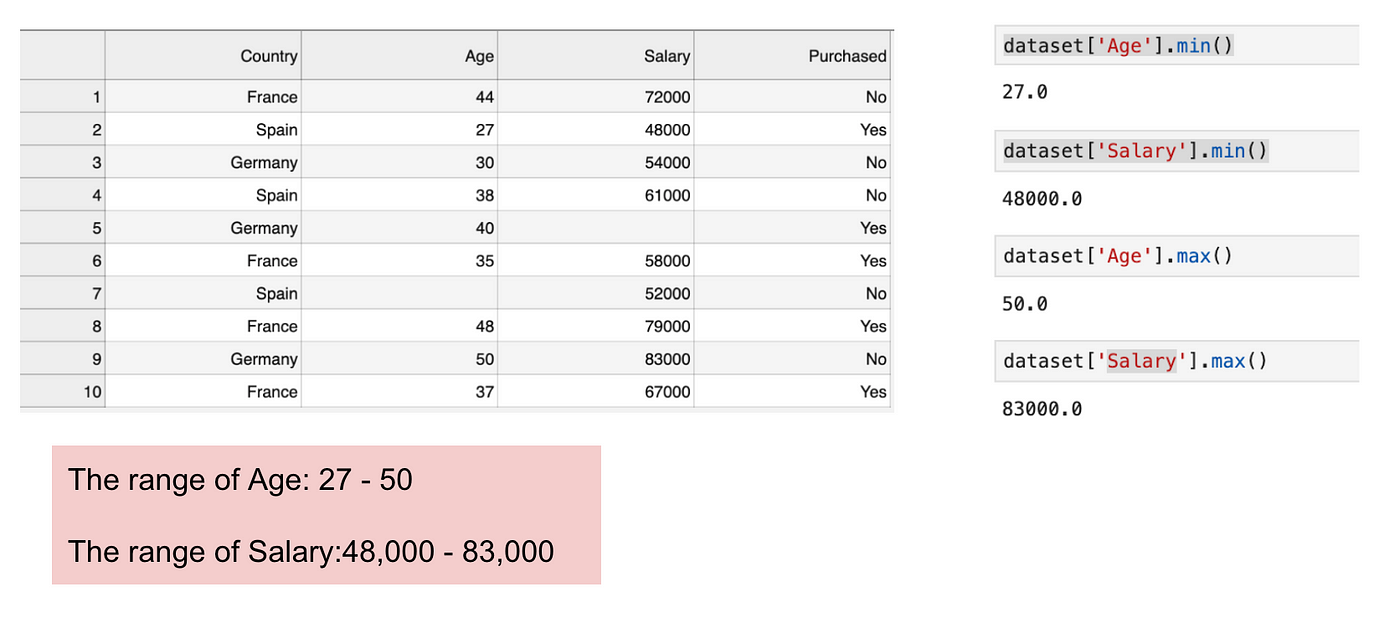
Skupiając się na wieku i wynagrodzeniu.
Gdy obliczamy równanie odległości euklidesowej, liczba (x2-x1)² jest znacznie większa niż liczba (y2-y1)², co oznacza, że odległość euklidesowa będzie zdominowana przez wynagrodzenie, jeśli nie zastosujemy skalowania cech. Różnica w wieku ma mniejszy udział w ogólnej różnicy. Dlatego powinniśmy zastosować skalowanie cech, aby sprowadzić wszystkie wartości do tych samych wielkości, a tym samym rozwiązać ten problem. Aby to zrobić, istnieją przede wszystkim dwie metody zwane Normalizacją i Normalizacją.

Zastosowanie odległości euklidesowej.
Standaryzacja
W wyniku normalizacji (lub normalizacji Z-score) cechy zostaną przeskalowane tak, aby średnia i odchylenie standardowe wynosiły odpowiednio 0 i 1. Równanie jest pokazane poniżej:
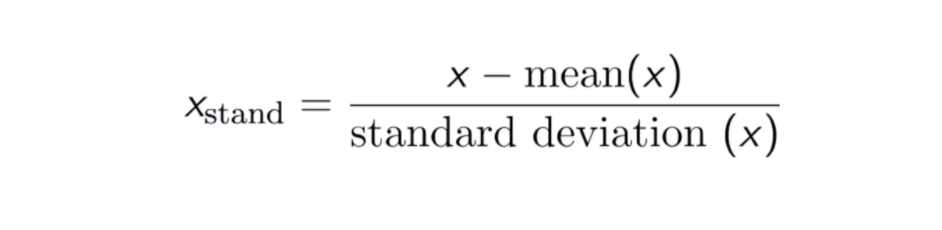
Ta technika jest do ponownego skalowania wartości cech z wartością dystrybucji między 0 i 1 jest przydatna dla algorytmów optymalizacji, takich jak gradient descent, które są używane w ramach algorytmów uczenia maszynowego, które ważą dane wejściowe (np. regresja i sieci neuronowe). Skalowanie jest również stosowane w algorytmach wykorzystujących pomiary odległości, na przykład K-Nearest-Neighbours (KNN).
Code
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Max-Min Normalization
Innym często stosowanym podejściem jest tak zwana Max-Min Normalization (skalowanie Min-Max). Technika ta polega na ponownym przeskalowaniu cech o wartości rozkładu pomiędzy 0 a 1. Dla każdej cechy wartość minimalna tej cechy zostaje przekształcona w 0, a wartość maksymalna w 1. Ogólne równanie jest przedstawione poniżej:
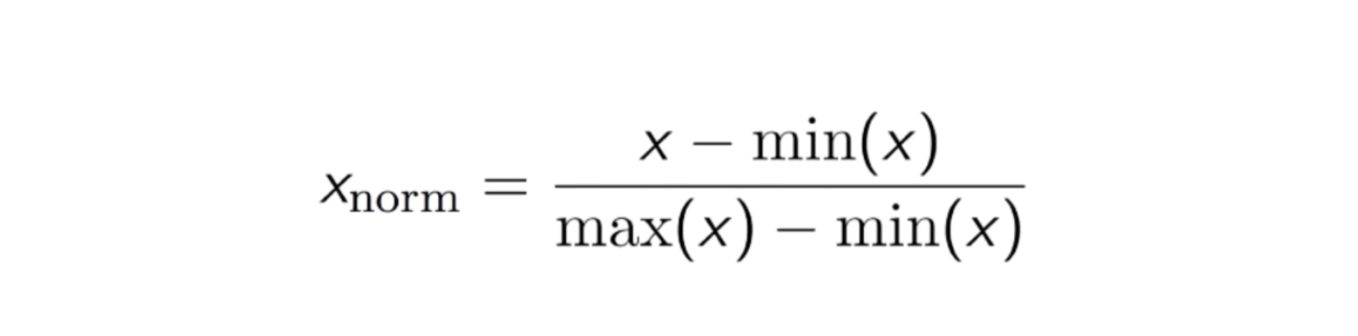
Równanie normalizacji Max-Min.
Kod
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
Standaryzacja vs Normalizacja Max-Min
W przeciwieństwie do normalizacji, poprzez proces Normalizacji Max-Min uzyskamy mniejsze odchylenia standardowe. Pozwól, że zilustruję więcej w tym obszarze używając powyższego zestawu danych.
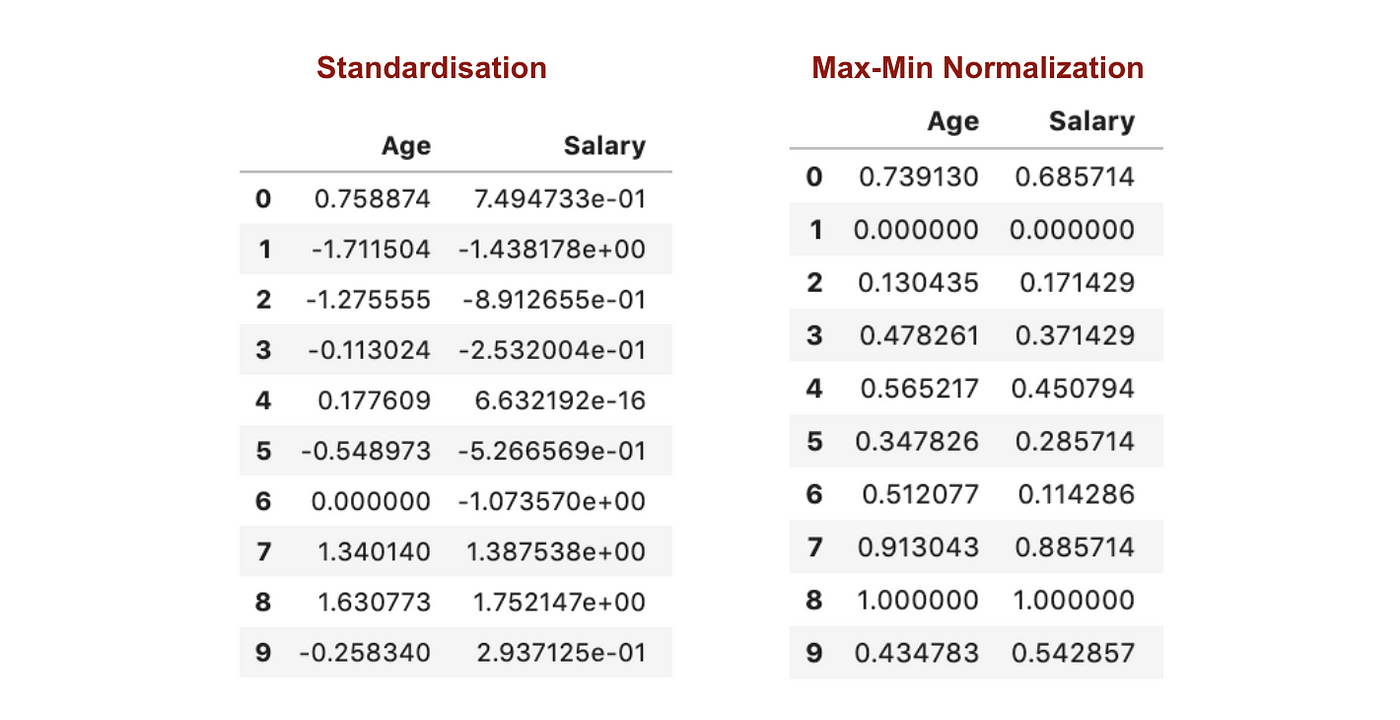
Po skalowaniu cech.

Rozkład normalny i odchylenie standardowe wynagrodzenia.
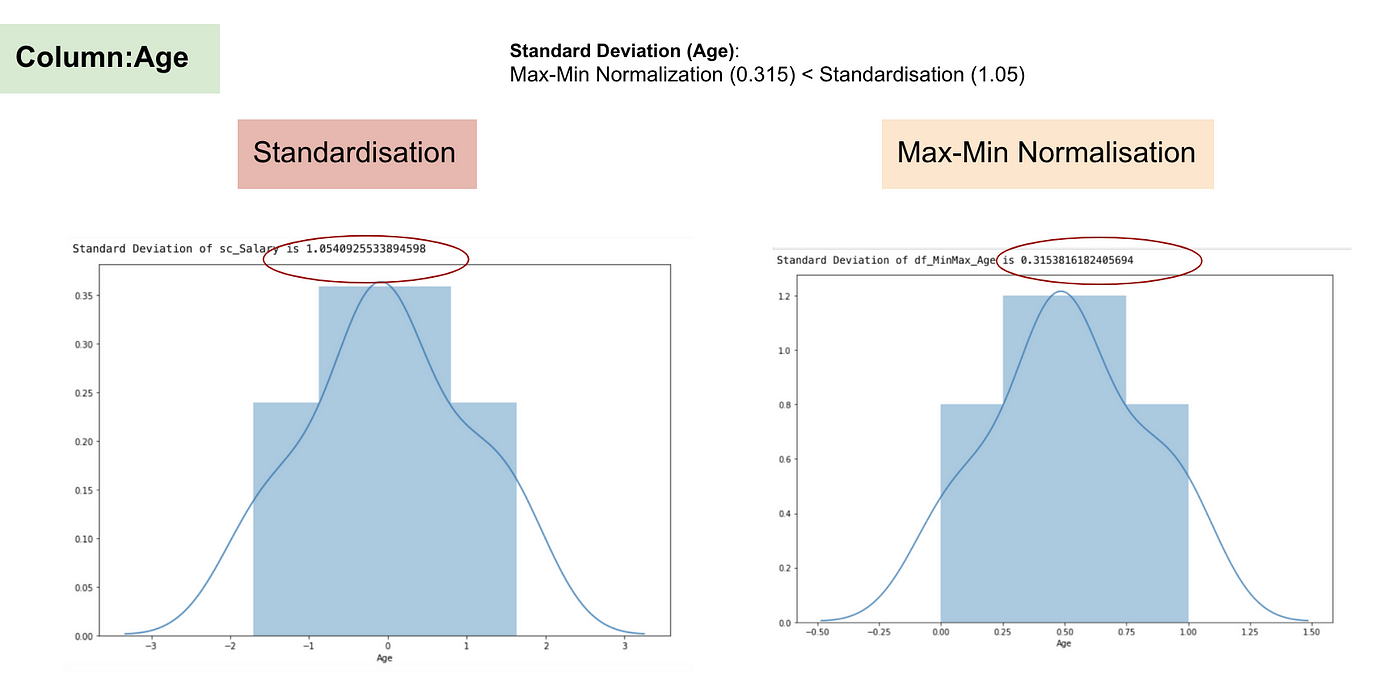
Rozkład normalny i odchylenie standardowe wieku.
Z powyższych wykresów można wyraźnie zauważyć, że zastosowanie Nomaryzacji Max-Min w naszym zbiorze danych wygenerowało mniejsze odchylenia standardowe (Wynagrodzenie i Wiek) niż zastosowanie metody Normalizacji. Sugeruje to, że dane są bardziej skoncentrowane wokół średniej, jeśli skalujemy dane przy użyciu Max-Min Nominalizacji.
W rezultacie, jeśli masz wartości odstające w swojej funkcji (kolumnie), normalizacja danych przeskaluje większość danych do małego przedziału, co oznacza, że wszystkie cechy będą miały tę samą skalę, ale nie obsługuje dobrze wartości odstających. Normalizacja jest bardziej odporna na wartości odstające i w wielu przypadkach jest preferowana w stosunku do normalizacji Max-Min.
Gdy skalowanie cech ma znaczenie

Niektóre modele uczenia maszynowego są zasadniczo oparte na macierzy odległości, znanej również jako klasyfikator oparty na odległości, na przykład K-Nearest-Neighbours, SVM i sieci neuronowe. Skalowanie cech jest niezwykle istotne dla tych modeli, szczególnie gdy zakres cech jest bardzo różny. W przeciwnym razie cechy o dużym zakresie będą miały duży wpływ na obliczanie odległości.
Max-Min Normalizacja zwykle pozwala nam przekształcić dane o różnych skalach tak, aby żaden konkretny wymiar nie zdominował statystyki, i nie wymaga przyjęcia bardzo silnego założenia o rozkładzie danych, jak w przypadku k-najbliższych sąsiadów i sztucznych sieci neuronowych. Normalizacja nie traktuje jednak zbyt dobrze outlinerów. Przeciwnie, normalizacja pozwala użytkownikom lepiej radzić sobie z wartościami odstającymi i ułatwia zbieżność dla niektórych algorytmów obliczeniowych, takich jak zejście gradientowe. Dlatego zwykle preferujemy normalizację nad normalizacją Min-Max.
Przykład: Jakie algorytmy potrzebują skalowania cech
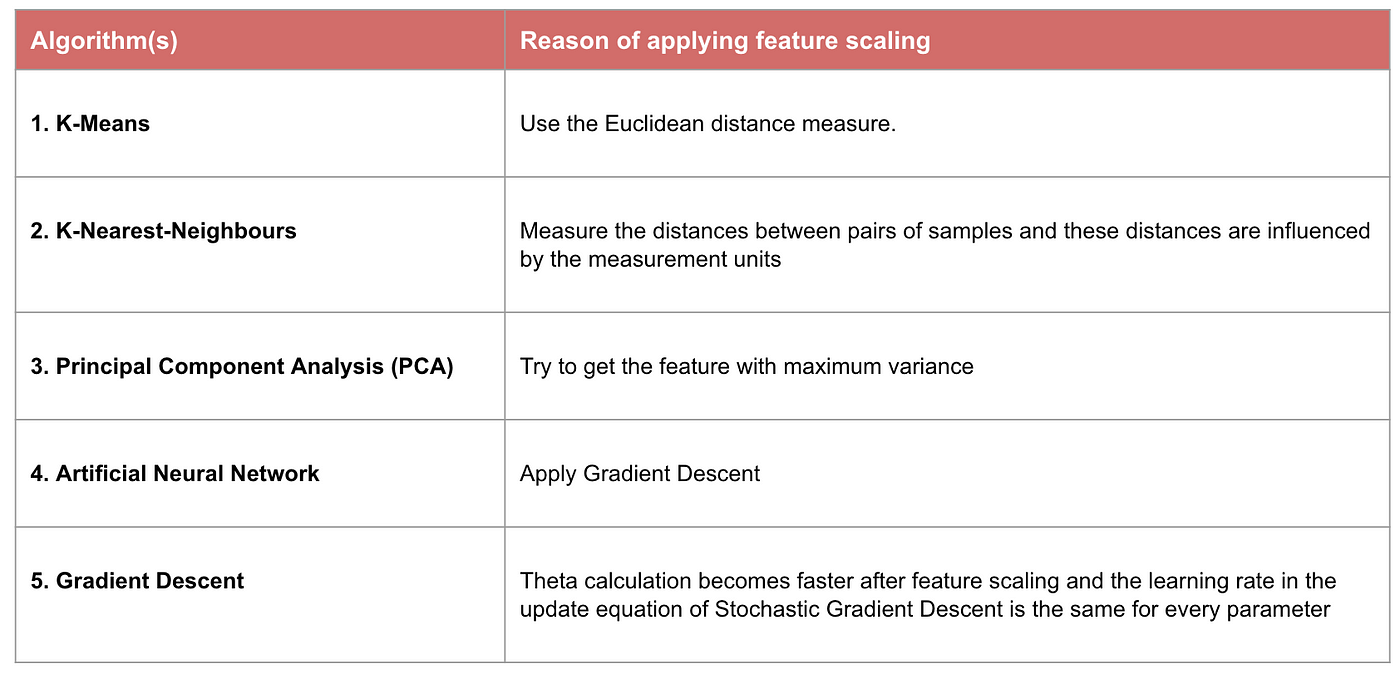
Uwaga: Jeśli algorytm nie jest oparty na odległości, skalowanie cech jest nieistotne, w tym Naive Bayes, Linear Discriminant Analysis i modele oparte na drzewach (gradient boosting, random forest, itp.).
Podsumowanie: Teraz powinieneś wiedzieć
- cel stosowania skalowania cech
- różnicę między normalizacją a normalizacją
- algorytmy, które muszą stosować normalizację lub normalizację
- stosowanie skalowania cech w Pythonie
Kod i zbiór danych znajdziesz tutaj.
.