
Az adatok átalakítása az adatfeldolgozás egyik alapvető lépése. Amikor először tanultam meg a jellemzők skálázásának technikáját, gyakran használták a skálázás, szabványosítás és normalizálás kifejezéseket. Elég nehéz volt azonban információt találni arról, hogy melyiket és mikor kell használnom. Ezért ebben a cikkben a következő főbb szempontokat fogom elmagyarázni:
- a standardizálás és a normalizálás közötti különbség
- mikor használjuk a standardizálást és mikor a normalizálást
- hogyan alkalmazzuk a feature skálázást Pythonban
Mit jelent a feature skálázás?
A gyakorlatban gyakran találkozunk különböző típusú változókkal ugyanabban az adathalmazban. Jelentős probléma, hogy a változók tartománya nagyon eltérő lehet. Az eredeti skála használata nagyobb súlyt helyezhet a nagy tartományú változókra. E probléma kezelése érdekében az adatok előfeldolgozásának lépésében a jellemzők átméretezésének technikáját kell alkalmaznunk az adatok független változóira vagy jellemzőire. A normalizálás és a standardizálás kifejezéseket néha felcserélve használják, de általában különböző dolgokra utalnak.
A Feature Scaling alkalmazásának célja, hogy a jellemzők közel azonos skálán legyenek, hogy minden egyes jellemző egyformán fontos legyen, és hogy a legtöbb ML-algoritmus könnyebben feldolgozhassa azokat.
Példa
Ez egy olyan adathalmaz, amely egy független változót (Purchased) és 3 függő változót (Country, Age, and Salary) tartalmaz. Könnyen észrevehetjük, hogy a változók nem azonos skálán helyezkednek el, mivel az Életkor tartománya 27 és 50 év között van, míg a Fizetés tartománya 48 K és 83 K között mozog. Ez problémákat okoz a modelljeinkben, mivel sok gépi tanulási modell, például a k-means klaszterezés és a legközelebbi szomszédok osztályozása az euklideszi távolságon alapul.
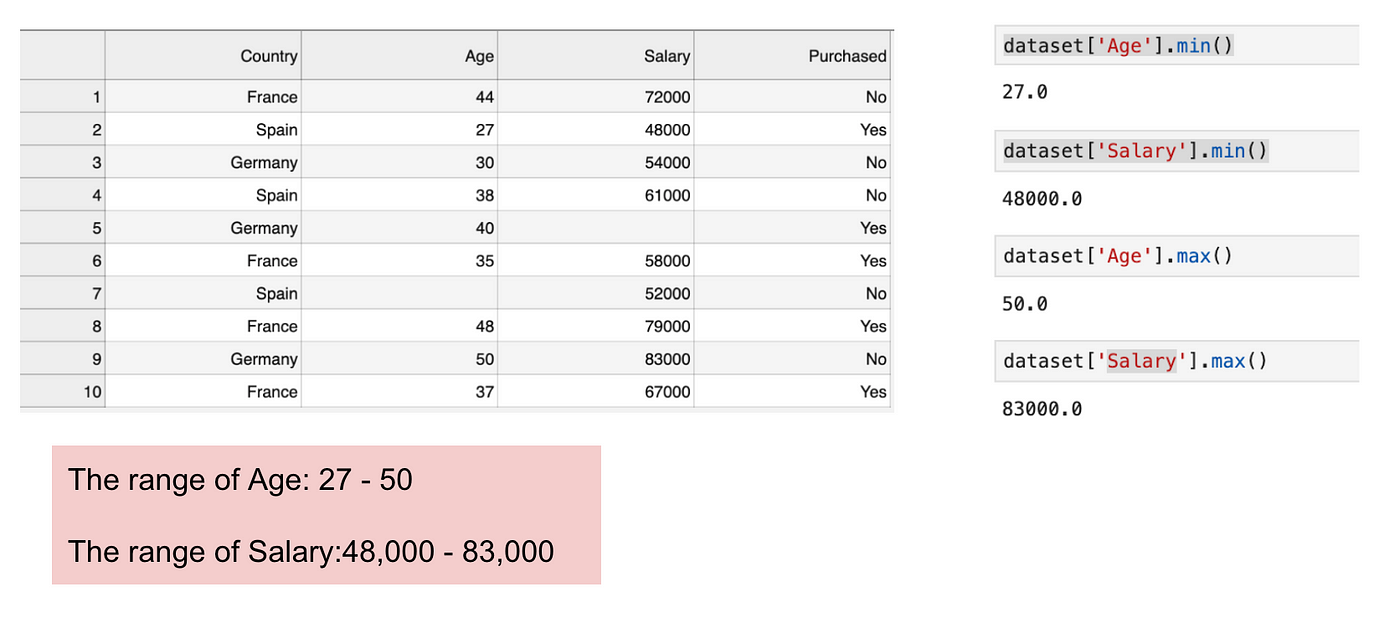
A korra és a fizetésre összpontosítva.
Az euklideszi távolság egyenletének kiszámításakor az (x2-x1)² száma sokkal nagyobb, mint az (y2-y1)² száma, ami azt jelenti, hogy az euklideszi távolságot a fizetés fogja uralni, ha nem alkalmazunk jellemzőskálázást. Az életkorbeli különbség kevésbé járul hozzá a teljes különbséghez. Ezért Feature Scalinget kell alkalmaznunk, hogy minden értéket azonos nagyságrendűvé tegyünk, és így megoldjuk ezt a problémát. Ehhez elsősorban két módszer áll rendelkezésre, a szabványosítás és a normalizálás.

Euklideszi távolság alkalmazása.
Standardizálás
A szabványosítás (vagy Z-pontszám normalizálás) eredménye az, hogy a jellemzőket átméretezzük, hogy az átlag és a szórás 0, illetve 1 legyen. Az egyenlet az alábbiakban látható:
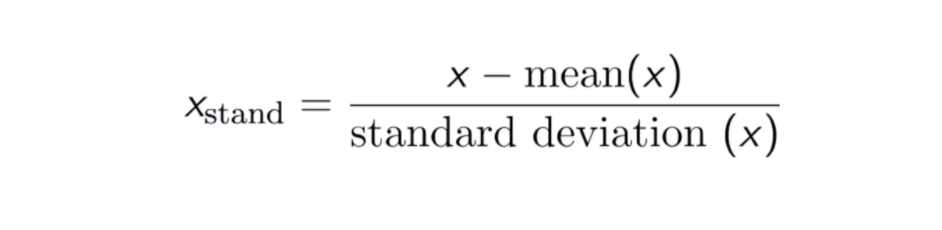
Ez a technika a jellemzők értékének 0 és 1 közötti eloszlási értékkel való újraszabályozása hasznos az optimalizációs algoritmusok, például a gradiens ereszkedés számára, amelyeket a bemeneteket súlyozó gépi tanulási algoritmusokban (pl. regresszió és neurális hálózatok) használnak. Az átskálázást a távolságméréseket használó algoritmusok, például a K-Nearest-Neighbours (KNN) esetében is alkalmazzák.
Code
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Max-Min Normalization
Egy másik gyakori megközelítés az úgynevezett Max-Min Normalization (Min-Max skálázás). Ez a technika a 0 és 1 közötti eloszlási értékkel rendelkező jellemzők átskálázását jelenti. Minden egyes jellemző esetében az adott jellemző minimális értéke 0-ra, a maximális érték pedig 1-re transzformálódik. Az általános egyenlet az alábbiakban látható:
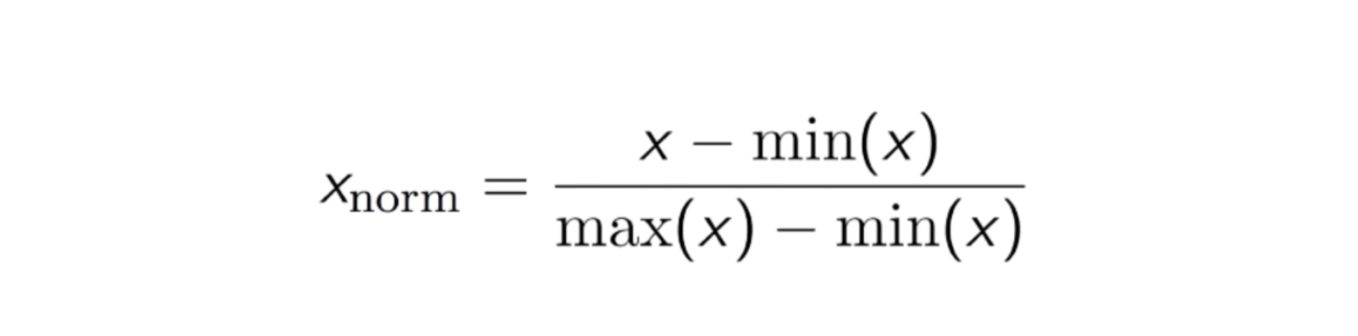
A Max-Min normalizáció egyenlete.
Kód
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
Standardizálás vs. Max-Min normalizálás
A standardizálással ellentétben a Max-Min normalizálással kisebb szórásokat kapunk. Hadd illusztráljak többet ezen a területen a fenti adatkészlet segítségével.
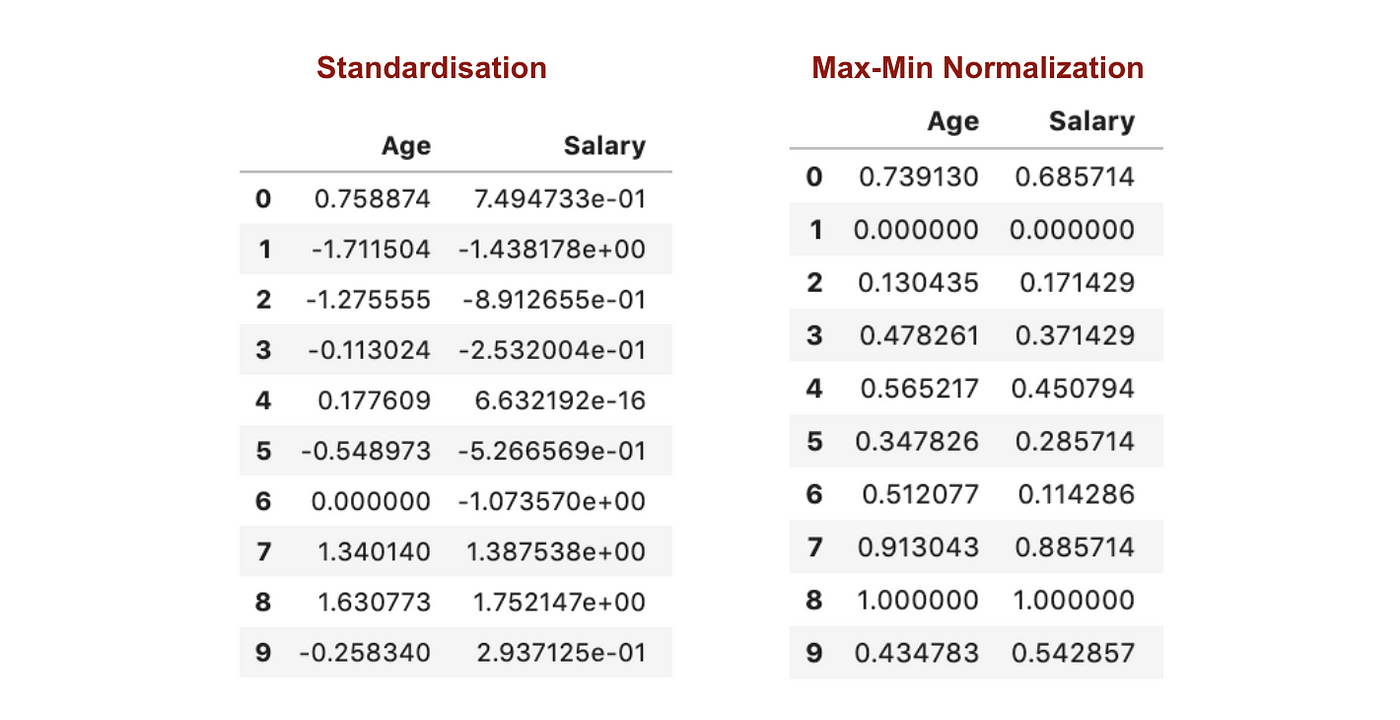
A Feature skálázás után.

Normális eloszlás és a fizetés szórása.
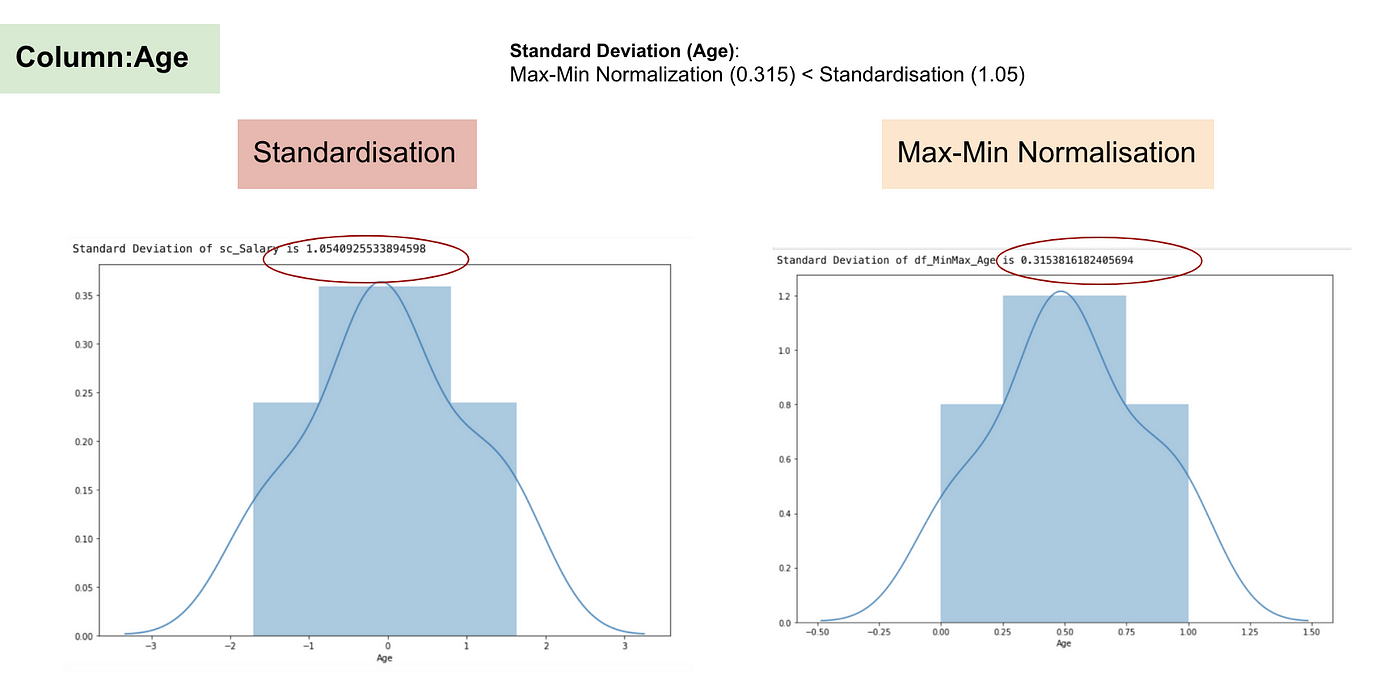
Normális eloszlás és a kor szórása.
A fenti grafikonokból jól látható, hogy a Max-Min Nomaralizáció alkalmazása az adatállományunkban kisebb szórásokat (Fizetés és Életkor) eredményezett, mint a Standardizációs módszer alkalmazása. Ez azt jelenti, hogy az adatok jobban koncentrálódnak az átlag körül, ha az adatokat Max-Min Nomaralizáció alkalmazásával skálázzuk.
Ez azt jelenti, hogy ha a jellemzőnkben (oszlopban) vannak kiugró értékek, akkor az adatok normalizálása az adatok nagy részét egy kis intervallumra skálázza, ami azt jelenti, hogy minden jellemzőnek ugyanaz lesz a skálája, de nem kezeli jól a kiugró értékeket. A normalizálás robusztusabb a kiugró értékekkel szemben, és sok esetben előnyösebb, mint a Max-Min normalizálás.
Mikor a jellemző skálázás számít

Egyes gépi tanulási modellek alapvetően távolságmátrixon alapulnak, más néven távolságalapú osztályozó, például a K-Nearest-Neighbours, az SVM és a neurális hálózat. A jellemzők skálázása rendkívül lényeges ezeknél a modelleknél, különösen akkor, ha a jellemzők tartománya nagyon eltérő. Ellenkező esetben a nagy tartományú jellemzők nagy hatással lesznek a távolság kiszámítására.
A Max-Min normalizálás jellemzően lehetővé teszi, hogy a különböző skálájú adatokat úgy alakítsuk át, hogy egyetlen konkrét dimenzió se domináljon a statisztikában, és nem kell nagyon erős feltételezést tenni az adatok eloszlásáról, mint például a k-közeli szomszédok és a mesterséges neurális hálózatok esetében. A normalizálás azonban nem kezeli túl jól a körvonalakat. Ezzel szemben a normalizálás lehetővé teszi a felhasználók számára, hogy jobban kezeljék a kiugró értékeket, és megkönnyíti egyes számítási algoritmusok, például a gradiens süllyedés konvergenciáját. Ezért általában előnyben részesítjük a normalizálást a Min-Max normalizálással szemben.
Példa: Milyen algoritmusoknak van szükségük jellemzőskálázásra
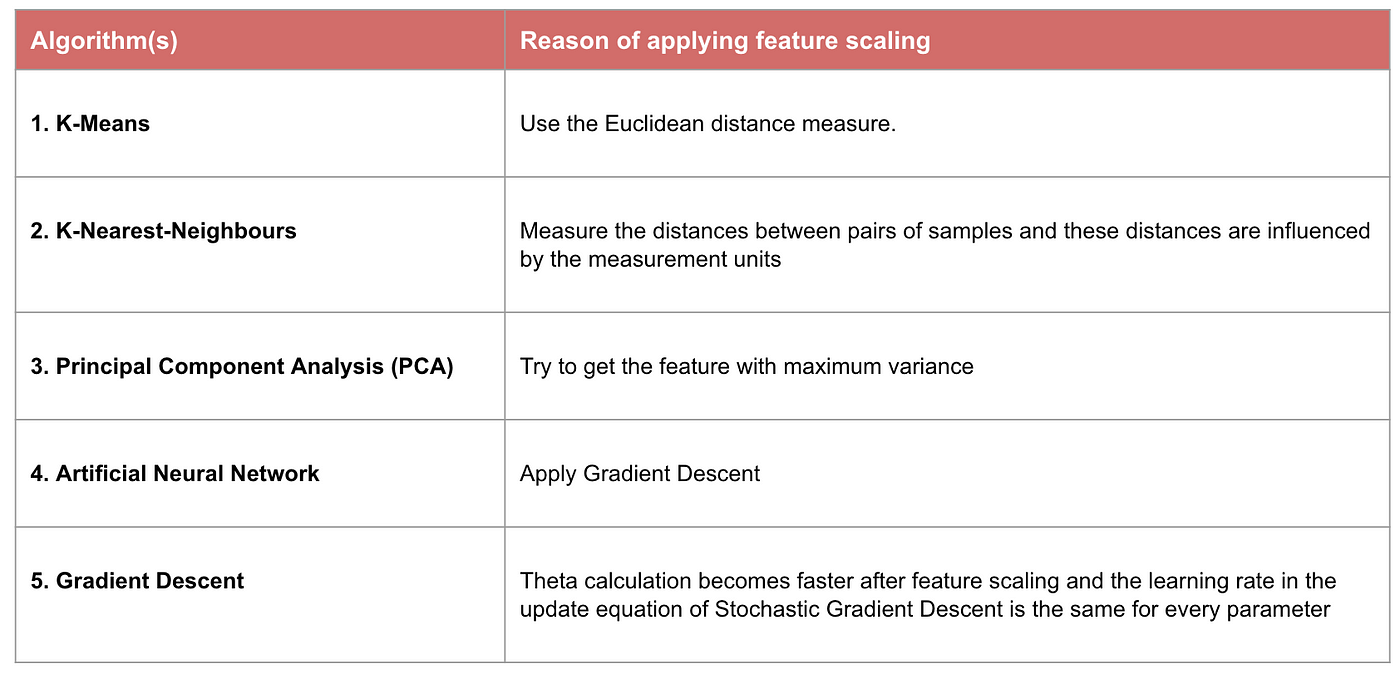
Megjegyzés: Ha egy algoritmus nem távolságalapú, a jellemzőskálázás nem fontos, beleértve a Naive Bayes-t, a lineáris diszkriminancia-elemzést és a faalapú modelleket (gradiens boosting, random forest stb.).
Összefoglaló: Most már tudnia kell
- a Feature Scaling alkalmazásának célját
- a Standardizáció és a Normalizáció közötti különbséget
- az algoritmusokat, amelyeknél Standardizációt vagy Normalizációt kell alkalmazni
- a Feature Scaling alkalmazása Pythonban
A kódot és az adatkészletet itt találja.