
La transformation des données est l’une des étapes fondamentales dans la partie du traitement des données. Lorsque j’ai appris pour la première fois la technique de mise à l’échelle des caractéristiques, les termes échelle, normalisation et normalisation sont souvent utilisés. Cependant, il était assez difficile de trouver des informations sur ceux que je devais utiliser et aussi quand les utiliser. Par conséquent, je vais expliquer les aspects clés suivants dans cet article :
- la différence entre la normalisation et la standardisation
- quand utiliser la standardisation et quand utiliser la normalisation
- comment appliquer la mise à l’échelle des caractéristiques en Python
Que signifie la mise à l’échelle des caractéristiques ?
Dans la pratique, nous rencontrons souvent différents types de variables dans le même ensemble de données. Un problème important est que la gamme des variables peut différer beaucoup. L’utilisation de l’échelle originale peut mettre plus de poids sur les variables avec une grande plage. Afin de résoudre ce problème, nous devons appliquer la technique de remise à l’échelle des caractéristiques aux variables indépendantes ou aux caractéristiques des données lors de l’étape de prétraitement des données. Les termes normalisation et standardisation sont parfois utilisés de manière interchangeable, mais ils font généralement référence à des choses différentes.
Le but de l’application de la mise à l’échelle des caractéristiques est de s’assurer que les caractéristiques sont sur presque la même échelle, de sorte que chaque caractéristique est d’importance égale et facilite le traitement par la plupart des algorithmes ML.
Exemple
C’est un ensemble de données qui contient une variable indépendante (Acheté) et 3 variables dépendantes (Pays, Âge et Salaire). Nous pouvons facilement remarquer que les variables ne sont pas sur la même échelle car la plage de l’âge est de 27 à 50, tandis que la plage du salaire va de 48 K à 83 K. La plage du salaire est beaucoup plus large que la plage de l’âge. Cela va causer quelques problèmes dans nos modèles puisque beaucoup de modèles d’apprentissage automatique tels que le clustering k-means et la classification du plus proche voisin sont basés sur la distance euclidienne.
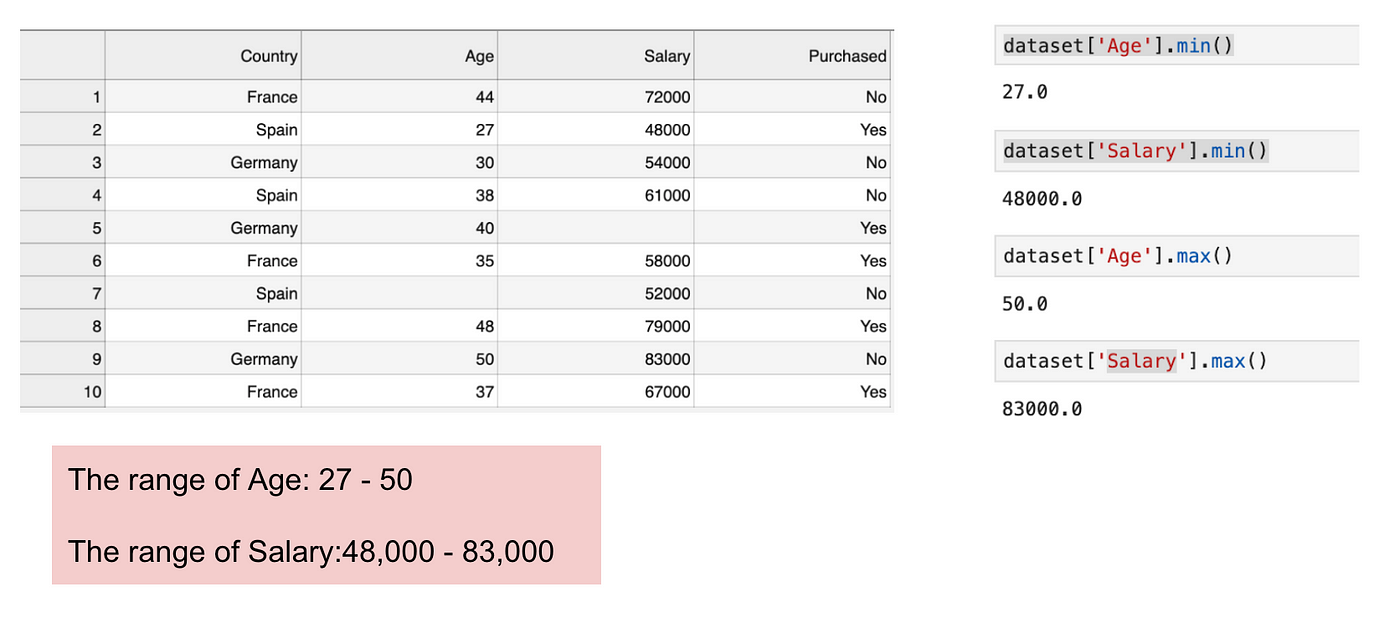
Focusing on age and salary.
Lorsque nous calculons l’équation de la distance euclidienne, le nombre de (x2-x1)² est beaucoup plus grand que le nombre de (y2-y1)² ce qui signifie que la distance euclidienne sera dominée par le salaire si nous n’appliquons pas l’échelonnement des caractéristiques. La différence d’âge contribue moins à la différence globale. Par conséquent, nous devrions utiliser la mise à l’échelle des caractéristiques pour amener toutes les valeurs aux mêmes magnitudes et, ainsi, résoudre ce problème. Pour ce faire, il existe principalement deux méthodes appelées Standardisation et Normalisation.

Application de la distance euclidienne.
Standardisation
Le résultat de la normalisation (ou normalisation du score Z) est que les caractéristiques seront remises à l’échelle pour que la moyenne et l’écart-type soient respectivement égaux à 0 et 1. L’équation est présentée ci-dessous :
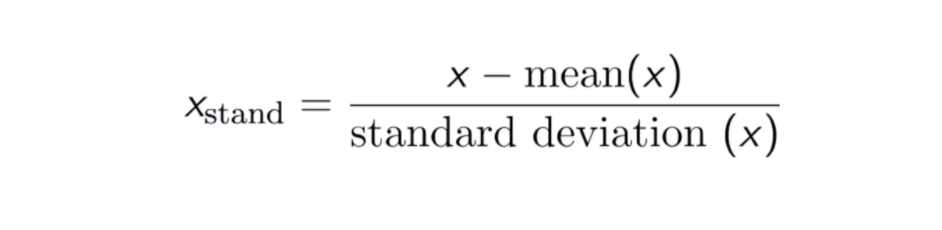
Cette technique consiste à remettre à l’échelle la valeur des caractéristiques avec la valeur de distribution entre 0 et 1 est utile pour les algorithmes d’optimisation, tels que la descente de gradient, qui sont utilisés au sein des algorithmes d’apprentissage automatique qui pondèrent les entrées (par exemple, la régression et les réseaux neuronaux). La remise à l’échelle est également utilisée pour les algorithmes qui utilisent des mesures de distance, par exemple, K-Plus Proches Voisins (KNN).
Code
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Normalisation Max-Min
Une autre approche courante est la normalisation dite Max-Min (mise à l’échelle Min-Max). Cette technique consiste à remettre à l’échelle des caractéristiques avec une valeur de distribution entre 0 et 1. Pour chaque caractéristique, la valeur minimale de cette caractéristique est transformée en 0, et la valeur maximale est transformée en 1. L’équation générale est présentée ci-dessous :
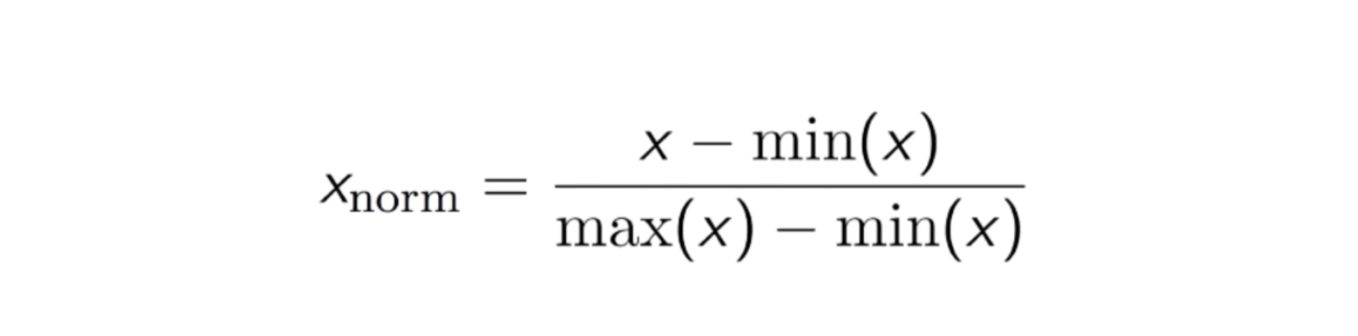
L’équation de la normalisation Max-Min.
Code
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
Standardisation vs Normalisation Max-Min
Contrairement à la standardisation, nous obtiendrons des écarts types plus petits grâce au processus de Normalisation Max-Min. Laissez-moi illustrer davantage dans ce domaine en utilisant l’ensemble de données ci-dessus.
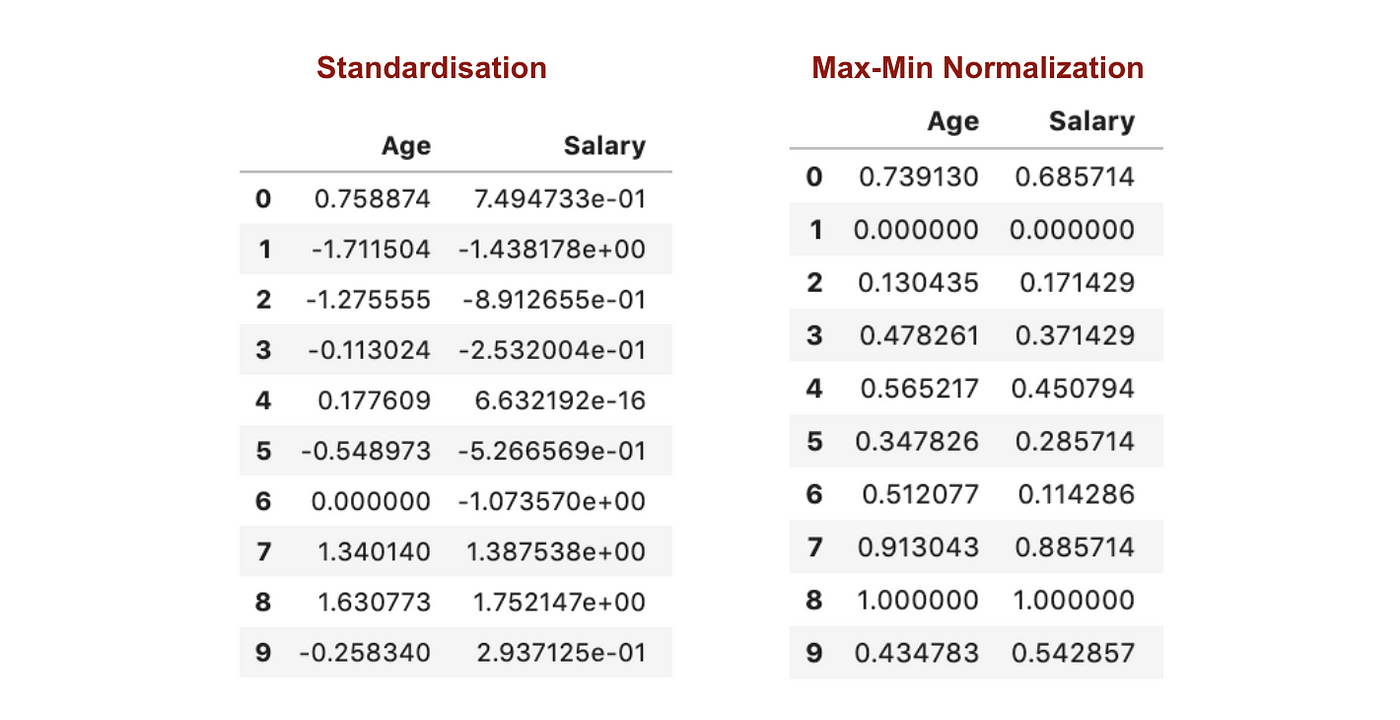
Après la mise à l’échelle des caractéristiques.

Distribution normale et écart-type du salaire.
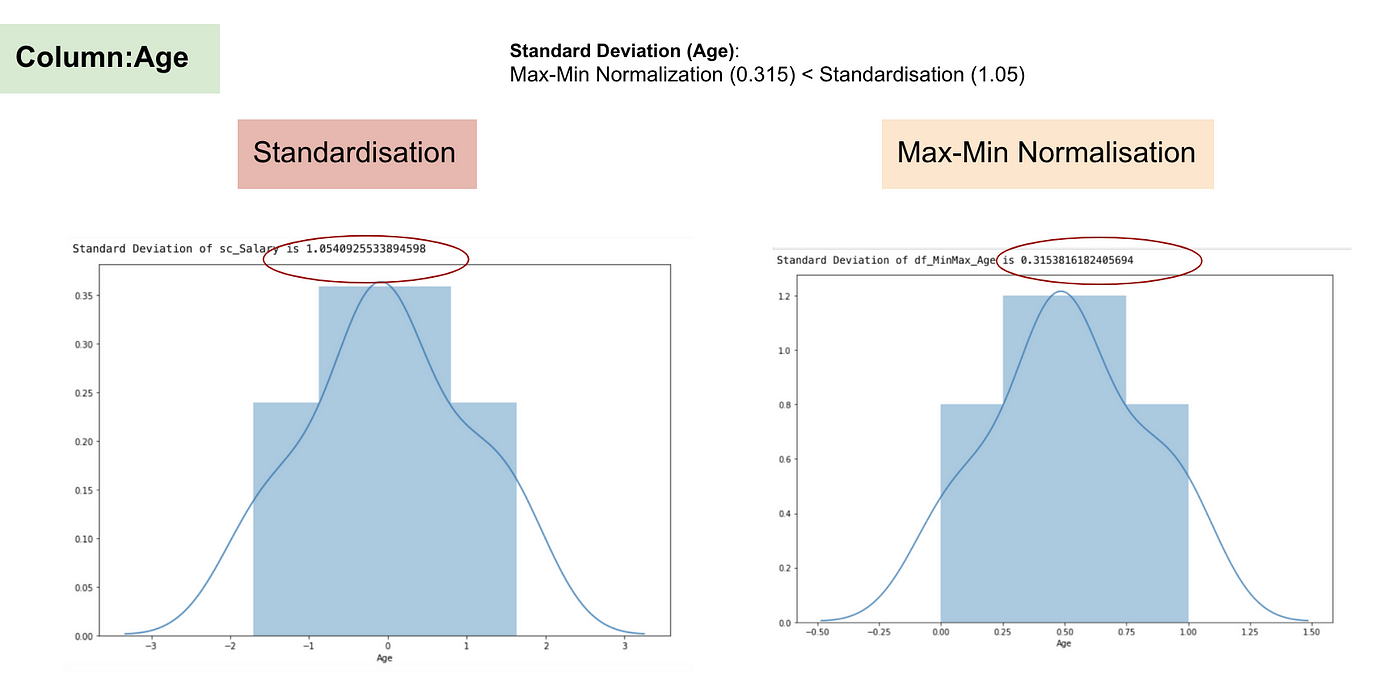
Distribution normale et écart-type de l’âge.
D’après les graphiques ci-dessus, nous pouvons clairement remarquer que l’application de la Nomaralisation Max-Min dans notre jeu de données a permis de réduire les écarts types (Salaire et Âge) par rapport à l’utilisation de la méthode de Standardisation. Cela implique que les données sont plus concentrées autour de la moyenne si nous mettons à l’échelle les données en utilisant la Nomaralisation Max-Min.
En conséquence, si vous avez des valeurs aberrantes dans votre caractéristique (colonne), la normalisation de vos données mettra à l’échelle la plupart des données à un petit intervalle, ce qui signifie que toutes les caractéristiques auront la même échelle mais ne gère pas bien les valeurs aberrantes. La normalisation est plus robuste aux valeurs aberrantes et, dans de nombreux cas, elle est préférable à la normalisation Max-Min.
Quand l’échelonnement des caractéristiques est important

Certains modèles d’apprentissage automatique sont fondamentalement basés sur la matrice de distance, également connue sous le nom de classificateur basé sur la distance, par exemple, K-Plus-Voisins, SVM et réseau neuronal. La mise à l’échelle des caractéristiques est extrêmement importante pour ces modèles, surtout lorsque la gamme des caractéristiques est très différente. Sinon, les caractéristiques avec une grande plage auront une grande influence dans le calcul de la distance.
La normalisation Max-Min nous permet généralement de transformer les données avec des échelles variables afin qu’aucune dimension spécifique ne domine les statistiques, et elle ne nécessite pas de faire une hypothèse très forte sur la distribution des données, comme les k-plus proches voisins et les réseaux de neurones artificiels. Cependant, la normalisation ne traite pas très bien les contours. Au contraire, la normalisation permet aux utilisateurs de mieux traiter les valeurs aberrantes et facilite la convergence pour certains algorithmes de calcul comme la descente de gradient. Par conséquent, nous préférons généralement la normalisation à la normalisation Min-Max.
Exemple : Quels algorithmes ont besoin d’une normalisation des caractéristiques
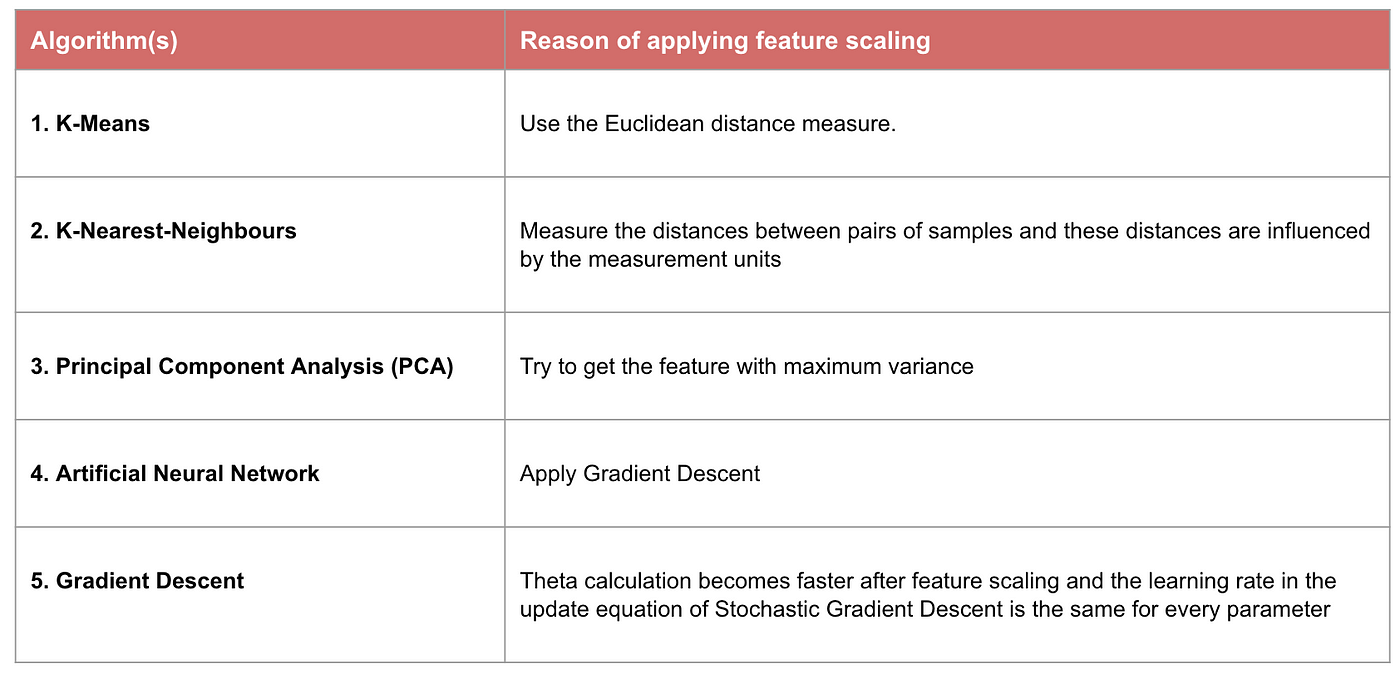
Note : Si un algorithme n’est pas basé sur la distance, la normalisation des caractéristiques n’est pas importante, y compris les Bayes naïfs, l’analyse discriminante linéaire et les modèles basés sur les arbres (gradient boosting, forêt aléatoire, etc.).
Résumé : Vous devriez maintenant connaître
- l’objectif de l’utilisation de la mise à l’échelle des caractéristiques
- la différence entre la normalisation et la standardisation
- les algorithmes qui ont besoin d’appliquer la standardisation ou la normalisation
- l’application de la mise à l’échelle des caractéristiques en Python
Veuillez trouver le code et le jeu de données ici.