
データ変換は、データ処理の一部における基本ステップの1つです。 私が最初に特徴スケーリングの技術を学んだとき、スケール、標準化、正規化という用語がよく使われました。 しかし、どれをどのタイミングで使えばいいのか、情報を探すのは結構大変でした。
- 標準化と正規化の違い
- 標準化を使うときと正規化を使うとき
- Pythonで特徴スケーリングを適用する方法
特徴スケーリングの意味
実際には、同じデータセットに異なるタイプの変数があることがよくあります。 重要な問題は、変数の範囲が大きく異なる場合があることです。 元の尺度を使用すると、範囲が大きい変数に重みがかかる可能性がある。 この問題に対処するために、データの前処理の段階で、独立変数またはデータの特徴に特徴量再スケーリングの技術を適用する必要があります。
特徴スケーリングを適用する目的は、特徴をほぼ同じ尺度にすることで、各特徴が等しく重要で、ほとんどのMLアルゴリズムで処理しやすくすることです。
例
これは、独立変数(購入)と3つの従属変数(国、年齢、給与)を含むデータセットである。 Ageの範囲が27から50で、Salaryの範囲が48Kから83Kなので、変数が同じ尺度でないことに簡単に気がつきます。 k-means クラスタリングや最近傍分類など、多くの機械学習モデルはユークリッド距離に基づいているため、これはモデルにおいていくつかの問題を引き起こすでしょう。
ユークリッド距離の式を計算すると、(x2-x1)²の数は(y2-y1)²の数よりはるかに大きく、これは特徴スケーリングを適用しなければユークリッド距離が給料に支配されることを意味します。 Ageの差は全体の差への寄与が少ないのです。 したがって、Feature Scalingを使用してすべての値を同じ大きさにすることで、この問題を解決する必要があります。 これを行うには、主に標準化と正規化という2つの方法があります。

ユークリッド距離の適用
標準化
標準化(またはZスコア正規化)の結果は、平均と標準偏差がそれぞれ0と1であるように特徴を再スケーリングすることです。 方程式を以下に示します:
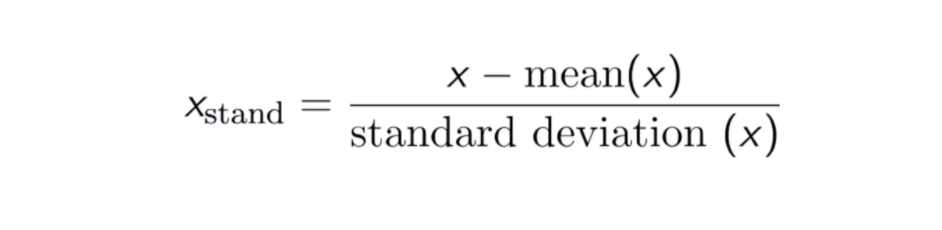
このテクニックは、0 と 1 の間の分布値で特徴値を再スケーリングすることで、入力に重み付けする機械学習アルゴリズム内で使用される勾配降下などの最適化アルゴリズム (たとえば、回帰およびニューラル ネットワーク) で有用です。 再スケーリングは、たとえば K-Nearest-Neighbours (KNN) のような距離測定を使用するアルゴリズムにも使用されます。
Code
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Max-Min Normalization
もう 1 つのよくあるアプローチは、いわゆる Max-Min Normalization (Min-Max scaling) です。 この手法は、0 から 1 の間の分布値で特徴を再スケーリングするものです。すべての特徴について、その特徴の最小値は 0 に変換され、最大値は 1 に変換されます。一般的な方程式を以下に示します。
Code
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
標準化と最大-最小正規化
標準化とは逆に、最大-最小正規化の過程では、小さい標準偏差を得ることになります。
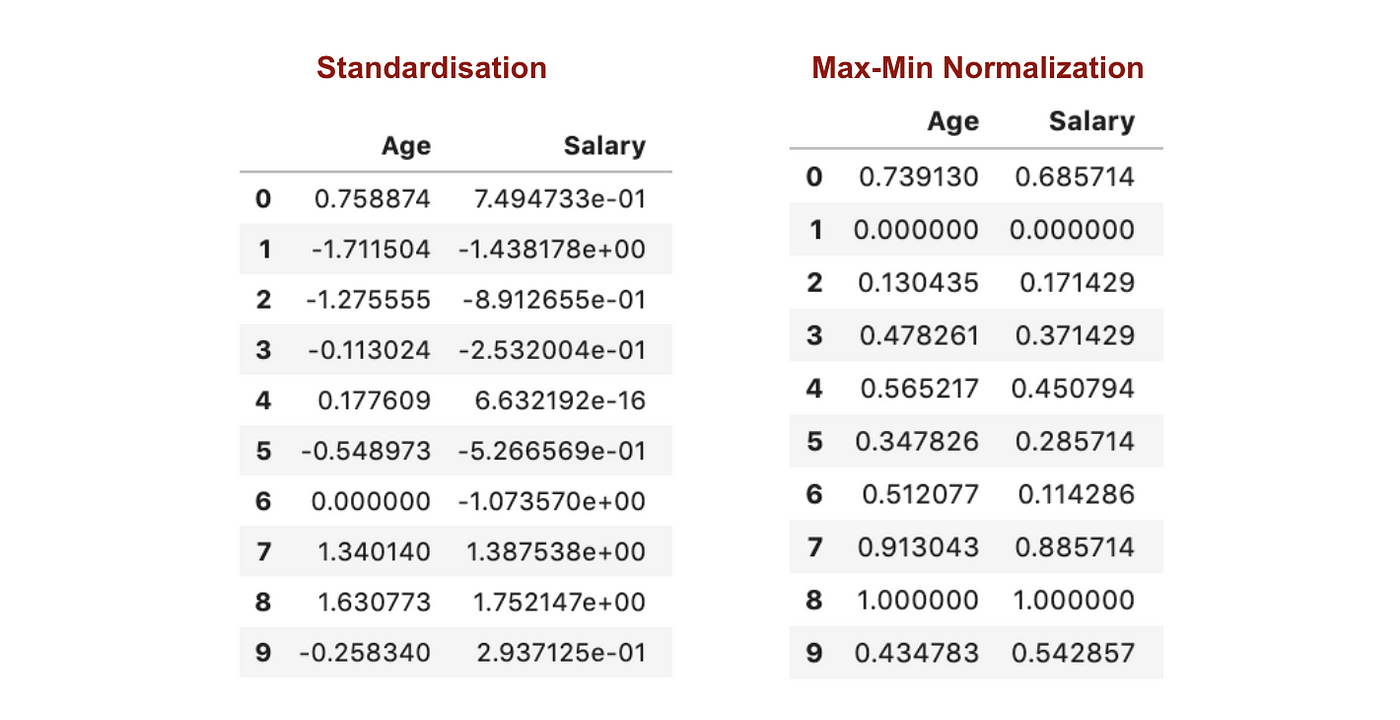
特徴量スケーリング後

正規分布と給与の標準偏差
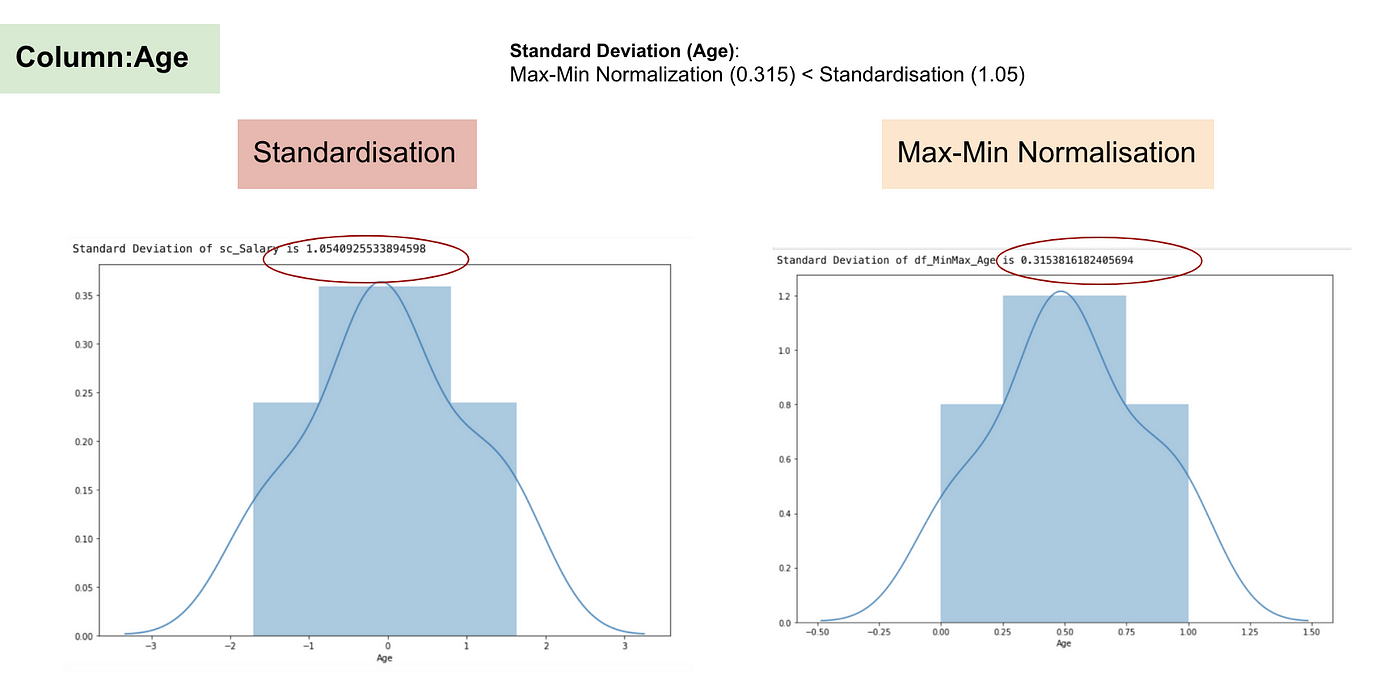
正規分布と年齢の標準偏差。
上記のグラフから、我々のデータセットにMax-Min Nomaralisationを適用すると、Standardisationメソッドを使用するよりも小さな標準偏差(SalaryとAge)を生成していることが明確にわかります。
その結果、特徴 (列) に外れ値がある場合、データを正規化すると、ほとんどのデータが小さな間隔にスケールされます。 標準化は外れ値に対してより堅牢であり、多くの場合、最大-最小正規化よりも望ましい。
When Feature Scaling matters

機械学習モデルの中には、K-最近傍、SVM、ニューラルネットワークなどの距離ベースの分類法として知られている、基本的に距離行列に基づくモデルがある。 特に特徴の範囲が大きく異なる場合、特徴のスケーリングはこれらのモデルにとって非常に重要である。 そうでなければ、範囲の大きい特徴が距離の計算で大きな影響を与えることになる。
Max-Min Normalisationは通常、特定の次元が統計量を支配することがないように、スケールの異なるデータを変換することができ、k-最近傍や人工ニューラルネットワークのように、データの分布について非常に強い仮定をする必要がない。 しかし、正規化ではアウトライナーをあまりうまく扱えません。 逆に、標準化によって、ユーザーは外れ値をうまく扱うことができ、勾配降下のような一部の計算アルゴリズムでは収束を促進することができます。 したがって、通常、Min-Max 正規化よりも標準化を優先します。
例。 どのようなアルゴリズムが特徴スケーリングを必要とするか
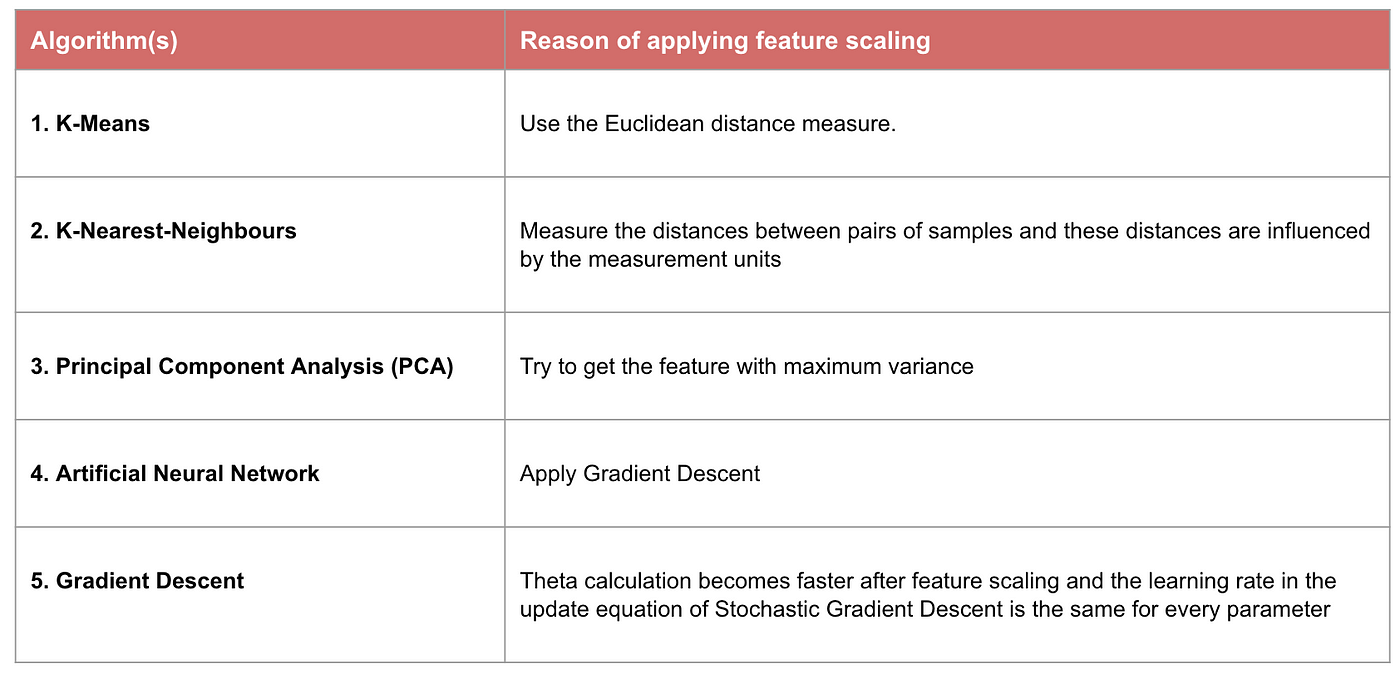
注意:アルゴリズムが距離ベースではない場合、ナイーブ ベイズ、線形判別分析、および木ベース モデル(勾配ブースティング、ランダム フォレストなど)などの特徴スケーリングは重要でありません。
概要:これで、
- 特徴スケーリングを使用する目的
- 標準化と正規化の違い
- 標準化または正規化を適用する必要があるアルゴリズム
- Pythonでの特徴スケーリングの適用
コードとデータセットはこちら
をご覧下さい。