
La transformación de datos es uno de los pasos fundamentales en la parte del procesamiento de datos. Cuando aprendí por primera vez la técnica del escalado de características, los términos escalar, estandarizar y normalizar se utilizan a menudo. Sin embargo, era bastante difícil encontrar información sobre cuál de ellos debía utilizar y también cuándo utilizarlo. Por lo tanto, voy a explicar los siguientes aspectos clave en este artículo:
- la diferencia entre Estandarizar y Normalizar
- cuándo usar Estandarizar y cuándo usar Normalizar
- cómo aplicar el escalado de características en Python
¿Qué significa el escalado de características?
En la práctica, a menudo nos encontramos con diferentes tipos de variables en el mismo conjunto de datos. Un problema importante es que el rango de las variables puede ser muy diferente. El uso de la escala original puede poner más peso en las variables con un rango grande. Para hacer frente a este problema, tenemos que aplicar la técnica de reescalado de características a las variables independientes o características de los datos en el paso de preprocesamiento de los datos. Los términos normalización y estandarización se utilizan a veces indistintamente, pero normalmente se refieren a cosas diferentes.
El objetivo de aplicar el reescalado de características es asegurarse de que las características están casi en la misma escala para que cada característica sea igual de importante y sea más fácil de procesar por la mayoría de los algoritmos de ML.
Ejemplo
Este es un conjunto de datos que contiene una variable independiente (Comprado) y 3 variables dependientes (País, Edad y Salario). Podemos notar fácilmente que las variables no están en la misma escala porque el rango de la Edad es de 27 a 50, mientras que el rango del Salario va de 48 K a 83 K. El rango del Salario es mucho más amplio que el de la Edad. Esto causará algunos problemas en nuestros modelos, ya que muchos modelos de aprendizaje automático, como la agrupación k-means y la clasificación del vecino más cercano, se basan en la distancia euclidiana.
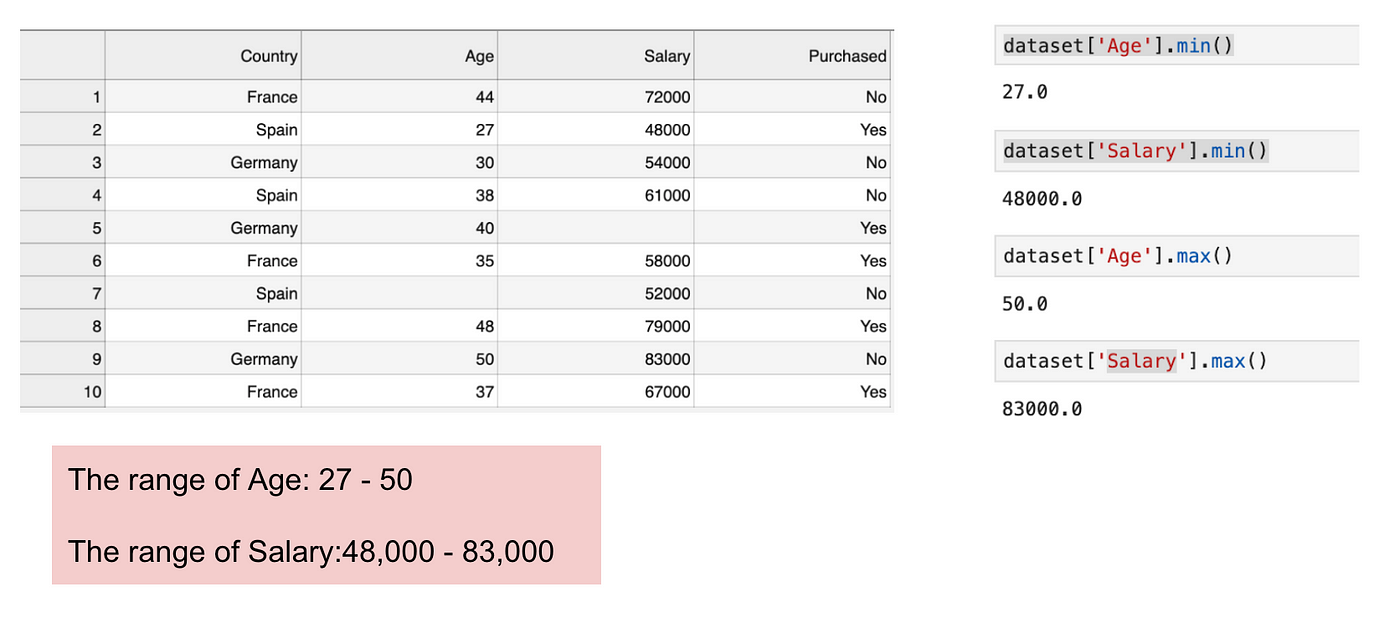
Enfocando la edad y el salario.
Cuando calculamos la ecuación de la distancia euclidiana, el número de (x2-x1)² es mucho mayor que el número de (y2-y1)² lo que significa que la distancia euclidiana estará dominada por el salario si no aplicamos el escalado de características. La diferencia de edad contribuye menos a la diferencia global. Por lo tanto, debemos utilizar el escalado de características para llevar todos los valores a las mismas magnitudes y, así, resolver este problema. Para ello, existen principalmente dos métodos denominados Estandarización y Normalización.

Aplicación de la distancia euclidiana.
Estandarización
El resultado de la estandarización (o normalización de la puntuación Z) es que las características se reescalarán para que la media y la desviación estándar sean 0 y 1, respectivamente. La ecuación se muestra a continuación:
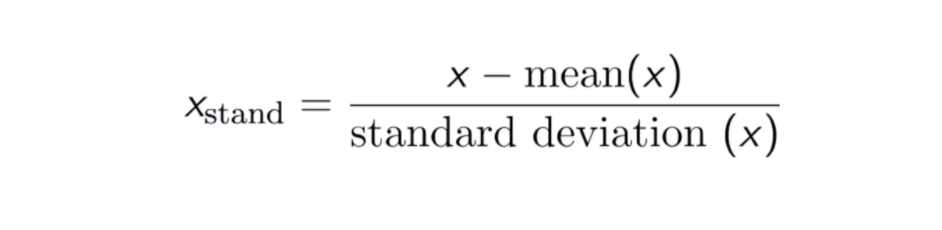
Esta técnica consiste en reescalar el valor de las características con el valor de la distribución entre 0 y 1 es útil para los algoritmos de optimización, como el descenso de gradiente, que se utilizan dentro de los algoritmos de aprendizaje automático que ponderan las entradas (por ejemplo, regresión y redes neuronales). El reescalado también se utiliza para los algoritmos que utilizan medidas de distancia, por ejemplo, K-Nearest-Neighbours (KNN).
Código
#Import libraryfrom sklearn.preprocessing import StandardScalersc_X = StandardScaler()sc_X = sc_X.fit_transform(df)#Convert to table format - StandardScaler sc_X = pd.DataFrame(data=sc_X, columns=)sc_X
Normalización Max-Min
Otro enfoque común es la llamada Normalización Max-Min (escalado Min-Max). Esta técnica consiste en reescalar características con un valor de distribución entre 0 y 1. Para cada característica, el valor mínimo de esa característica se transforma en 0, y el valor máximo se transforma en 1. La ecuación general se muestra a continuación:
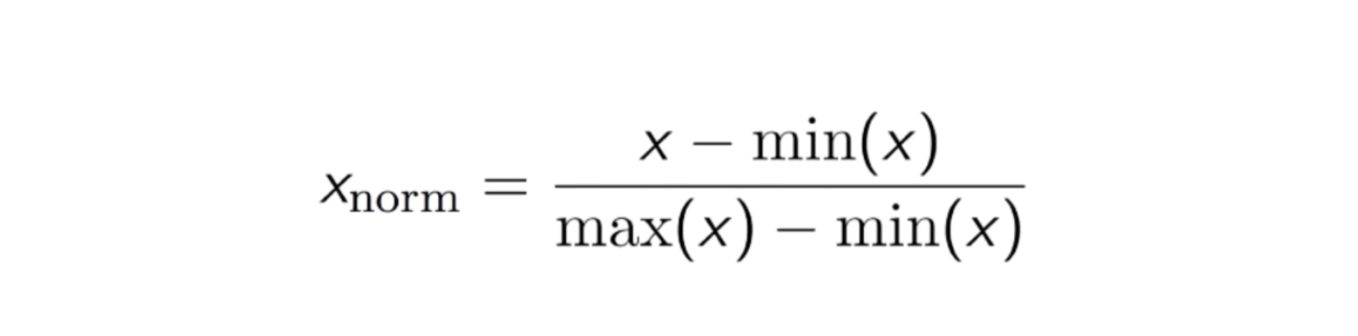
La ecuación de la Normalización Max-Min.
Código
from sklearn.preprocessing import MinMaxScalerscaler = MinMaxScaler()scaler.fit(df)scaled_features = scaler.transform(df)#Convert to table format - MinMaxScalerdf_MinMax = pd.DataFrame(data=scaled_features, columns=)
Estandarización vs Normalización Max-Min
En contraste con la estandarización, obtendremos desviaciones estándar más pequeñas a través del proceso de Normalización Max-Min. Permítanme ilustrar más en esta área utilizando el conjunto de datos anterior.
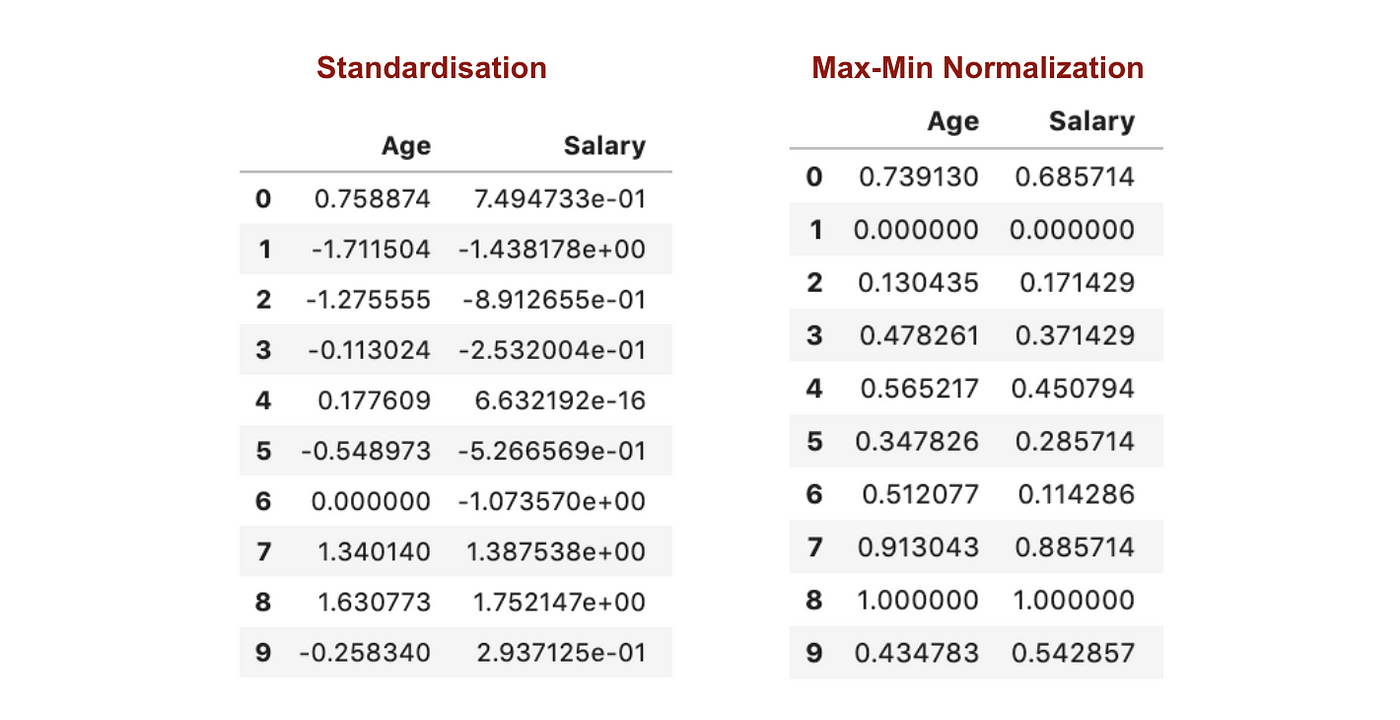
Después del escalado de características.

Distribución normal y desviación estándar del salario.
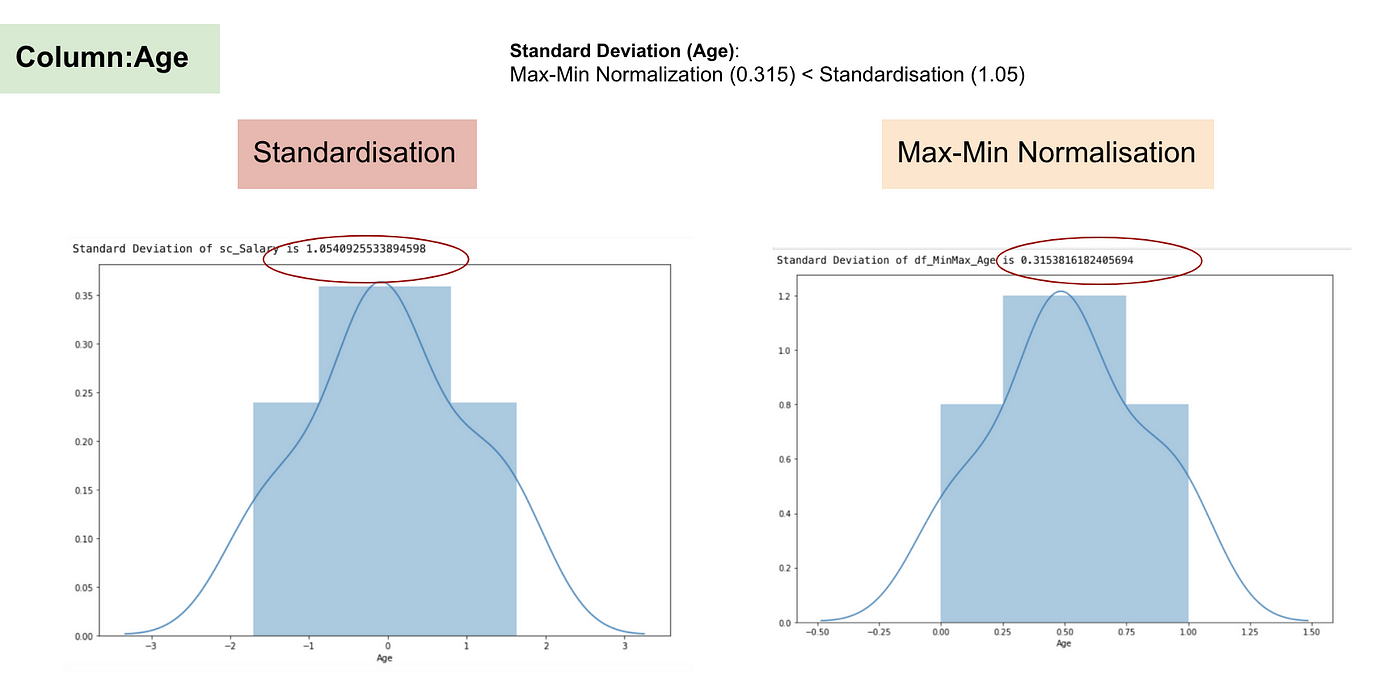
Distribución normal y desviación estándar de la edad.
De los gráficos anteriores, podemos observar claramente que la aplicación de la Nomaralización Max-Min en nuestro conjunto de datos ha generado desviaciones estándar más pequeñas (Salario y Edad) que utilizando el método de Estandarización. Esto implica que los datos están más concentrados alrededor de la media si escalamos los datos utilizando la Nomaralización Max-Min.
Como resultado, si tiene valores atípicos en su característica (columna), la normalización de sus datos escalará la mayoría de los datos a un pequeño intervalo, lo que significa que todas las características tendrán la misma escala pero no maneja bien los valores atípicos. La normalización es más robusta a los valores atípicos, y en muchos casos, es preferible a la Normalización Max-Min.
Cuando el escalado de características es importante

Algunos modelos de aprendizaje automático se basan fundamentalmente en la matriz de distancia, también conocido como el clasificador basado en la distancia, por ejemplo, K-Nearest-Neighbours, SVM, y Red Neural. El escalado de características es extremadamente esencial para esos modelos, especialmente cuando el rango de las características es muy diferente. De lo contrario, las características con un gran rango tendrán una gran influencia en el cálculo de la distancia.
La Normalización Máxima-Mínima normalmente nos permite transformar los datos con escalas variables para que ninguna dimensión específica domine las estadísticas, y no requiere hacer una suposición muy fuerte sobre la distribución de los datos, como los vecinos más cercanos K y las redes neuronales artificiales. Sin embargo, la normalización no trata muy bien los contornos. Por el contrario, la normalización permite manejar mejor los valores atípicos y facilita la convergencia de algunos algoritmos computacionales como el descenso de gradiente. Por lo tanto, solemos preferir la normalización a la Normalización Min-Max.
Ejemplo: Qué algoritmos necesitan el escalado de características
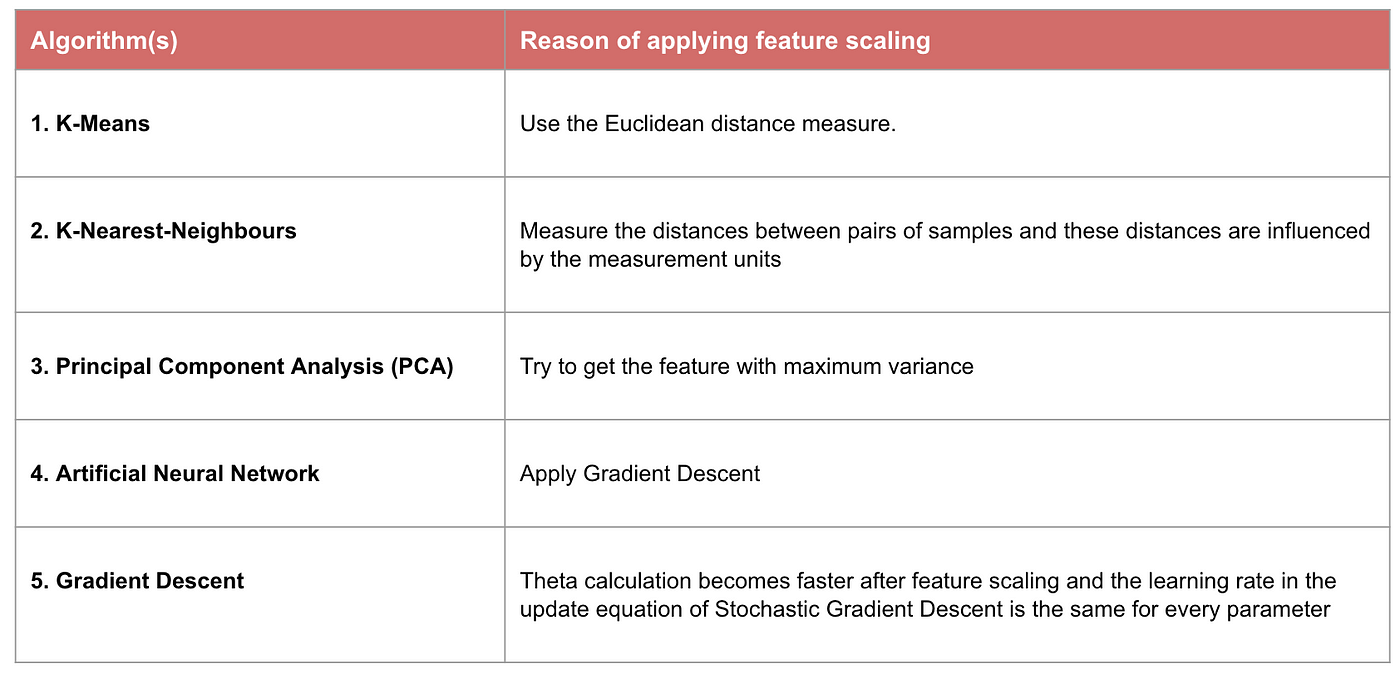
Nota: Si un algoritmo no está basado en la distancia, el escalado de características no es importante, incluyendo Naive Bayes, el análisis discriminante lineal y los modelos basados en árboles (gradient boosting, random forest, etc.).
Resumen: Ahora debe saber
- el objetivo de utilizar el escalado de características
- la diferencia entre normalización y normalización
- los algoritmos que necesitan aplicar normalización o normalización
- aplicar el escalado de características en Python
Por favor, encuentre el código y el conjunto de datos aquí.